התייחסות והבנה מעמיקה של כל המאפיינים של פונקציה רציונלית . 

בחינת הבחירה הנכונה של הפרמטרים הנכונים במשימות החקירה של פונקציה רציונלית המתאימות לתוכנית הלימודים ברמה של 5 יחידות . ומטרה חשובה נוספת היא מפגש חקירת הפונקציה בצורה הקונבינציונלית בעזרת דף ועפרון עם חקירת הפונקציה בעזרת כלים הטכנולוגיים – גיאוגברה . ואז תהיה הטמעה מלאה לכל הידע התיאורטי שרכש התלמיד .

הפעילות הזו יכולה להתאים לתלמידי כתה י' בסוף השנה אם בתוכנית שלהם נמצאת " חקירת פונקציה רציונלית " . אבל מומלץ לבצע אותה בכיתה י"א – השנה שבה התלמידים ייגשו לבחינת הבגרות בפונקציות רציונליות .

עיתוי הפעילות 

הפעילות הזו יכולה להתבצע  בכיתה כסיכום של נושא " חקירת פונקציה רציונלית " . בשלב כזה לאחר שיש לתלמידים את כל הידע התיאורטי ואת כל הכלים הדרושים לחקירת פונקציה רציונלית , יהיה למפגש עם הטכנולוגיה ערך מוסף מעבר למידת נושא . יהיה מעניין להסתכל על התלמידים , על הפנים שלהם כשהם מקבלים החלטה נכונה והחיוך שאחריו . כמו כן  כל תלמיד יהיה בטוח יותר בידע שלו לאחר פעילות כזו . והקטע הכי חשוב הוא השיח המתמטי שהתפתח בין התלמידים תוך כדי הפעילות , ושיח כזה שונה מהשיח שעשוי להתפתח בעקבות פעילות שהיא פתיחת נושא . 

תחום הגדרה של פונקציה רציונאלית, אסימפטוטות מקבילות לצירים, נקודות אי רציפות סליקה של הפונקציה, חיתוך עם הצירים, פתרון משוואות פרמטריות.

1. בפעילות הזו התעורר שיח מעניין מאוד בין התלמידים . רוב השיח נסוב סביב משימה מס' 2 שבה התבקשו להתייחס לקיומן של אסימפטוטות אנכיות 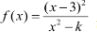לפונקציה  וסביב משימה מס' 3 הדנה במספר נקודות החיתוך עם ציר ה- x  . המיוחד בפונקציה כזו הוא שיש לה נקודת סליקה במקרה של K=9  , הויכוח התמקד בשאלה האם בכל זאת לפונקציה יש חיתוך עם ציר ה- x  כי ראו בגיאוגברה סימן לקיומו של חיתוך כזה . ואז עלתה האבחנה בין נקודת סליקה מרחפת לבין נקודת סליקה הנמצאת ממש על הציר .
2. התעורר הויכוח סביב צמצום הפונקציה במקרה של K=9  , והישארותו של הביטוי (x-3)  במונה גם לאחר הצמצום . לכן הייתי מוסיף לשורת המשימות את חקירת הפונקציה    ואז ההטמעה של האסימפטוטות ונקודות הסליקה תהיה מושלמת , במיוחד שכל עניין ההרכבות של פונקציה על פונקציה נעשה פופולרי בקרב מחברי בחינות הבגרות ברמה של 5 יחידות .
3. הרחבת הכלים של התוכנה כדי שתכלול את כל הסל של הפעולות שניתן לבצע על פונקציה , וזה יכלול את כל סוגי ההזזות , את העלאת הפונקציה בריבוע , את הפיכת הסימן של הפונקציה ואת היפוכה . 

הטענות 1, 2, 3, 4 נכונות/ לא נכונות.

נקודות חשובות לדיון לאחר ביצוע משימה:

משימה 1:

עוסקת בתחום ההגדרה של הפונקציה. משימה במערכת המראה דורשת הבנה מעמיקה יותר  בנושא על ידי חלוקה לפי המקרים עם התייחסות לערכי פרמטר k:

הפונקציה מוגדרת לכל x

הפונקציה מוגדרת לכל x, פרט ל-0

הפונקציה מוגדרת לכל x, פרט ל-3

הפונקציה מוגדרת לכל x, פרט לx=3  ו- x=-3

על התלמיד להגיש מסך תומך לכל טענה שהיא נכונה, ולכן לא קיים מקרה שעבורו פונקציה נתונה מוגדרת לכל x , פרט ל-3. ולכן מקרה זה דורש דיון כיתתי על השטיח  של תשובות התלמידים. חשוב להדגיש סימון אסימפטוטות אנכיות ואופקית בשרטוט של גרף הפונקציה.

משימה 2:

מתמקדת באסימטוטות של הפונקציה. הדגש יותר על אסימפטוטה אנכית, כי קיימים מקרים שונים בהתאם לתחום ההגדרה של הפונקציה וגם עבור ערכי k  שונים. כמובן בדיון לאחר ביצוע משימה חשוב לשאול : מהי אסימפטוטה אופקית?

 (בפונקציה נתונה יש אסימפטוטה אופקית y=1, אין מקרים נוספים.)  

משימה 3:

נקודות חשובות לדיון עם תלמידים לאחר ביצוע משימה לפונקציה. האם קיים מקרה כזה שאין נקודות חיתוך עם ציר ה-x ?

אם כן, עבור איזה ערך של ? k

במשימה זו לרשותו של תלמיד יש את כלים לבנייה נוחה וקלה של שרטוט הגרף, אך עדיין על מנת לקבל תשובה נכונה חשוב לשים לב לתחום ההגדרה של הפונקציה. לקבוע מהן אסימפטוטות ונקודת אי-רציפות סליקה ולהדגיש אותן על הגרף. 

משימה 4:

נקודות חשובות לדיון עם תלמידים לאחר ביצוע משימה. 

לפונקציה נקודות חיתוך אחת עם ציר ה-Y: האם קיים מקרה כזה ועבור איזה ערך ? K

לפונקציה אין נקודות חיתוך עם ציר ה-Y: האם קיים מקרה כזה ועבור איזה ערך ? K