הקדמה כללית: 

עפיפון דלתון מקורו במלזיה. סוחרים ומגלי ארצות ייבאו אותו משם לאירופה. דגם זה של העפיפון הצליח בשוק המקומי כי היה קל לבנות אותו ופשוט להעיף אותו באוויר. בנוסף לכך, עפיפון מדגם זה היה מאד יציב במהירויות שונות של עוצמת הרוח.

אם רוצים להשתמש בעפיפון כזה בגובה רב צריך לבצע מספר שינויים: כמו להזיז את נקודת הגרירה- הנקודה שבה החוט קשור למפרש, ולקצר או להגדיל את אורך הזנב.

המבנה של עפיפון כזה מורכב מיריעה בצורת של דלתון ושני מקלות שמחוברים זה לזה בהצלבה. הדלתון הוא סימטרי ביחס לאלכסון הראשי שלו, דבר זה עוזר ליציבות של עפיפון דלתון. מאפיין נוסף של עפיפון דלתון היא היכולת שלו לרחף ללא זנב.

החלק העליון של עפיפון דלתון הוא תמיד המשולש הקטן והחלק התחתון הוא המשולש הגדול יותר. חלקו התחתון של הדלתון נראה כמו משולש הפוך, כך שהוא הולך ונעשה צר יותר ככל שמגיעים לקצה למטה ובאופן מסוים זה כמו תחליף לזנב.

האלכסון הראשי של עפיפון דלתון מכונה שדרה והאלכסון המשני מכונה קולב.

בעפיפון דלתון  השדרה יכולה  להיות קצרה מהקולב או שווה באורכה לאורך הקולב.

מקור תמונה: www.lia.co.il

הקדמה למשימות:

בכל הקייטנות העירוניות בארץ החליטו להעביר סדנת לבניית עפיפוני דלתון. כל הילדים התבקשו לבנות עפיפונים שהמפרש שלהם בצבע ירוק והזנב שלהם כתום. ביום האחרון של הקייטנה תכננו  לערוך מסיבה סיום שבה הילדים יעיפו את העפיפונים שבנו אל על ויכסו את שמי הארץ בעפיפונים בעלי אותו הצבע.

בכל אחת מהקייטנות  "משחקיה", "אליהו" ו"נוגה" החליטו שכל הילדים באותה קייטנה יבנו עפיפונים שווים בגודלם – כלומר עפיפונים בעלי אותו שטח מפרש. זאת כדי למנוע תחרות בין הילדים וויכוחים מי מהם בנה עפיפון גדול יותר.  

המטרה של משימות 1-3 היא לאפשר לתלמידים לחקור ולהגיע למסקנה שהשטח של דלתון תלוי באורכי האלכסונים שלו.

במשימה 1 נתון כי בקייטנת "שעשוע" הזמינו מארגני הקייטנה כמות גדולה של מקלות בשני אורכים 50 ס"מ ו- 60 ס"מ. הילדים בקייטנה יכולים לבחור שני מקלות כלשהם מבין המקלות שהוזמנו כך שאחד מהמקלות ישמש כשדרה והאחר כקולב בעפיפון שיבנו.

כמו כן נתונות טענות. התלמיד מתבקש להגיש דוגמה תומכת לכל טענה. 

1. קיים דלתון שהוא בעל שטח מפרש הכי גדול.
2. קיים עפיפון שהוא בעל שטח מפרש קטן ביותר.
3. קיים עפיפון שהוא בעל שטח מפרש שונה משני העפיפונים בטענות הקודמות.

ביישומון, התלמידים יכולים לבחור את אורך השדרה של העפיפון ואת אורך הקולב בסנטימטרים ולהזיז את הנקודה הכחולה כדי לשנות את מיקום החיבור בין השדרה לקולב.

במשימה 2 נתון כי בקייטנת "משחקיה", כל אחד מהילדים קיבל מקל אחד באורך 56 ס"מ ומקל שני באורך 38 ס"מ. אחד מהמקלות שימש כשדרה והשני כקולב בעפיפון שבנו.

כמו כן נתונה טענה:

הילדים בקייטנת "משחקיה" יכולים לבנות עפיפונים שונים  ששווים בשטח המפרש שלהם.

התלמיד מתבקש להחליט אם הטענה נכונה או לא,  אם בחרו כן הם מתבקשים להגיש 3 דוגמאות לעפיפונים ששווים בשטח המפרש שלהם שיכולים להתקבל בקייטנת "משחקיה". אם בחרו לא, הם מתבקשים להגיש 3 דוגמאות לעפיפונים שסותרים את הטענה.

ביישומון, התלמידים יכולים לבחור את אורך השדרה של העפיפון ואת אורך הקולב בסנטימטרים ולהזיז את הנקודה הכחולה כדי לשנות את מיקום החיבור בין השדרה לקולב.

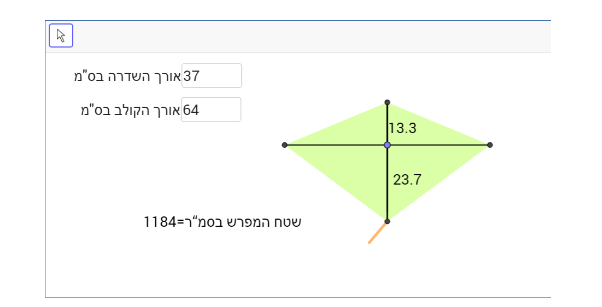
במשימה 3 נתון כי בקייטנת "אליהו" רוצים לבנות עפיפונים ששטח המפרש שלהם 1800 סמ"ר. כל ילד בקייטנה יכול לבחור את אורך השדרה ואת אורך הקולב בעפיפון שלו ובהתאם לכך יספקו לו את המקלות הדרושים לבניית העפיפון. כמו כן  ביקשו מהילדים שאורך השדרה וגם אורך הקולב לא יעלו על 100 ס"מ ואורכם לא יהיה פחות מ-25 ס"מ.

התלמידים מתבקשים להגיש 3 דוגמאות לאורכים שונים של השדרה והקולב שילדים יכולים לבחור ודוגמה לעפיפון שהם יכולים לבנות באמצעות השדרה והקולב שבחרו.

ביישומון, התלמידים יכולים לבחור את אורך השדרה של העפיפון ואת אורך הקולב בסנטימטרים ולהזיז את הנקודה הכחולה כדי לשנות את מיקום החיבור בין השדרה לקולב.

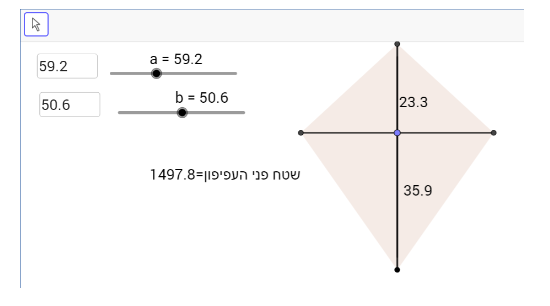
במשימה 4 נתון כי בקייטנת "נוגה" החליטו שכל התלמידים יבנו עפיפונים ששטח מפרשם הוא 1250 סמ"ר. כל ילד בקייטנה יכול לבחור את אורך השדרה ואת אורך הקולב בעפיפון שלו ובהתאם לכך יספקו לו את המקלות הדרושים לבניית העפיפון. כמו כן ביקשו מהילדים בקייטנה שאורך השדרה וגם אורך הקולב בעפיפון שלהם  לא יעלו על 100ס"מ ואורכם לא יהיה פחות מ-25   ס"מ.

נתונות טענות. התלמידים מתבקשים להגיש לכל טענה דוגמה תומכת.

1. בקייטנת נוגה תלמידים יכולים לבנות עפיפון שצורתו ריבוע
2. בקייטנת נוגה תלמידים יכולים לבנות עפיפון שצורתו מעוין
3. בקייטנת נוגה תלמידים יכולים לבנות עפיפון שצורתו טרפז

  המטרה של משימה 4  היא יישום הידע על תכונות של מרובעים (ריבוע, מעויין, טרפז) או ללמוד אותן (לתלמידים שלא למדו).

במשימה 5 נתון כי בקייטנת "אביבית" אפשרו לילדים לבנות עפיפונים שונים בשטח המפרש שלהם  אבל גם בקשו שאורך השדרה וגם אורך הקולב לא יעלו על 100 ס"מ ואורכם לא יהיה פחות מ-25 ס"מ. כמו כן ביקשו שבמפרש של העפיפון תהיה לפחות זווית ישרה אחת. ­­­

נתונות טענות. התלמידים מתבקשים לסמן את הטענות הנכונות, ולכל טענה נכונה להגיש דוגמה תומכת של עפיפון דלתון מתאים על ידי כתיבת מידות השדרה והקולב שלו ואת המרחק של מפגש המקלות מהקודקוד העליון של העפיפון.

1. אפשר לבנות עפיפון שיש לו זווית ישרה אחת בלבד 
2. אפשר לבנות עפיפון שיש לו בדיוק שתי זוויות ישרות.
3. אפשר לבנות עפיפון בעל 3 זוויות ישרות בלבד
4. אפשר  לבנות עפיפון בעל 4 זויות ישרות

המטרה של משימה 5 היא להשתמש בידע על דמיון משולשים, ידע על תכונות משולש בעל הזוויות 30-60-90, וידע על תכונות הדלתון. 

שני הנושאים "משולש שווה שוקיים" ו-"דמיון משולשים" נלמדים בכיתה ח' כך שלפי תוכנית הלימודים "יש ללמוד למצוא נתונים חסרים מתוך תכונת הדמיון ותוך שימוש בפרופורציה….כמו כן, יש לעסוק בבעיות המשלבות בין דמיון משולשים ובין עובדות שנלמדו בכיתה ז' ובתחילת כיתה ח' , תוך שילוב דוגמאות מחיי היומיום" (ראו תוכנית הלימודים – עמ' 71  + 88 ) 

נושא "דלתון ומשולש שווה שוקיים"  נלמד בכיתה ט' כך שלפי תוכנית הלימודים "יש לנצל את הוראת הדלתון כדי לתרגל היסק הנוגע לחפיפת משולשים ולמשולש שווה שוקיים, או לנושאים אחרים שנלמדו בעבר" כמו כן, "במסגרת לימוד על הדלתון, יש לחזור על משפטים העוסקים במשולשים שווי שוקיים" (מתוך תוכנית הלימודים – עמ' 181)

לכן פעילות "בונים עפיפונים" מתאימה כפעילות תרגול לתלמידים בכיתות ח'-ט' אשר למדו את הנושאים האלה.

תכונות של מרובעים (דלתון, טרפז, מעויין, ריבוע)

דמיון משולשים (אפשר גם להשתמש במשפט תאלס – לא חובה)  

חישובי שטחים (משולש שווה שוקיים ודלתון) 

תכונות משולשים מיוחדים (שווה צלעות, שווה שוקיים, משולש הזהב 30-60-90)

משימה 1

טענה 1 :  עפיפון בעל שטח מפרש הכי גדול  הוא העפיפון הבנוי משדרה באורך 60 ס"מ וגם קולב באורך 60 ס"מ 

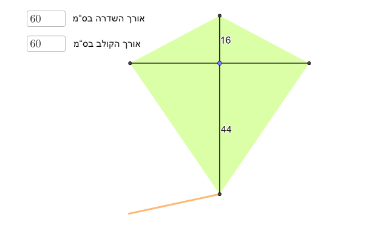
טענה 2: עפיפון בעל שטח מפרש קטן ביותר הוא העפיפון הבנוי משדרה באורך 50 ס"מ וגם קולב באורך 50 ס"מ 

טענה 3 : עפיפון בעל שטח מפרש שונה משני העפיפונים בטענות הקודמות הוא העפיפון הבנוי משדרה באורך 60 ס"מ וקולב באורך 50 ס"מ , או שדרה באורך 50 ס"מ וקולב באורך 60 ס"מ 

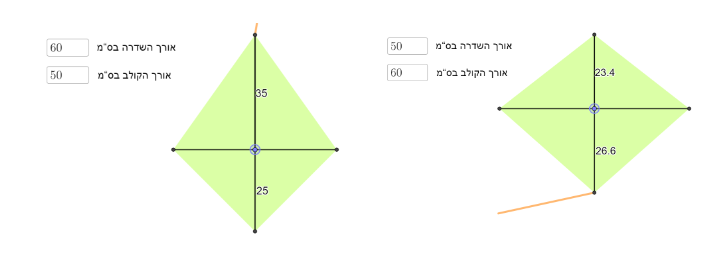
משימה 2 

הטענה נכונה.

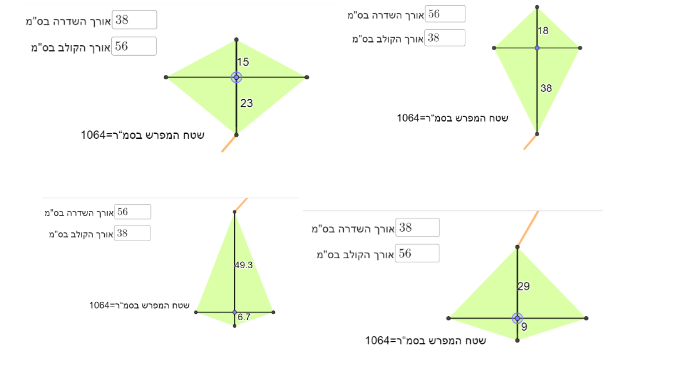
משימה 3

משימה 4    

טענה 1: נכונה – קייטנת "נוגה" תלמידים יכולים לבנות עפיפון שצורתו ריבוע

למשל:

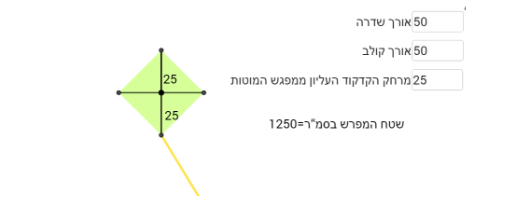
טענה 2: לא נכונה (בקייטנת "נוגה" תלמידים לא יכולים לבנות עפיפון שצורתו טרפז)

טענה 3: נכונה – בקייטנת "נוגה" תלמידים יכולים לבנות עפיפון שצורתו מעוין

למשל: 

משימה 5

טענה 1: נכונה – אפשר לבנות עפיפון שיש לו זווית ישרה אחת בלבד (המשולש העליון הוא משולש ישר זווית ושווה שוקיים)

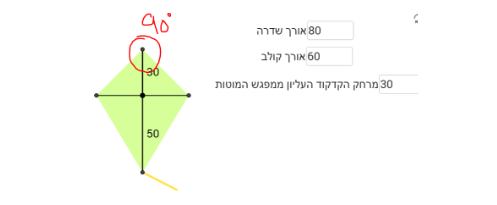
טענה 2: נכונה – אפשר לבנות עפיפון שיש לו בדיוק שתי זוויות ישרות (החצי של הקולב בריבוע צריך להיות שווה למכפלת הקטעים של השדרה) 

טענה 3: לא נכונה ( אי-אפשר לבנות עפיפון שיש לו בדיוק 3 זוויות ישרות)

טענה 4: נכונה – אפשר לבנות עפיפון שיש לו 4 זוויות ישרות  (העפיפון בצורת ריבוע – המשולש העליון הוא משולש שווה צלעות וגם המשולש התחתון הוא שווה צלעות)

משימה 1

הקולב יותר ארוך מהשדרה 

הקולב והשדרה שווים באורכם

הצורה היא ריבוע 

הצורה היא מעויין

השתמשו במקלות באורכים אחרים מהנתונים

משימה 2

הקולב והשדרה שונים באורכם

הקולב יותר ארוך מהשדרה 

הצורה היא ריבוע 

הצורה היא מעויין

השתמשו במקלות באורכים אחרים מהנתונים

משימה 3

הוגשה דוגמה מתאימה לדרישות המשימה

האורך קטן מ 100 וגדול מ 25 

הקולב יותר ארוך מהשדרה 

הצורה היא ריבוע 

הצורה היא מעויין

הקולב והשדרה שונים באורכם

השתמשו במספרים שלמים

משימה 4

לכל אחת מהטענות:

השטח מקיים את הדרישה 

האורך קטן מ 100 וגדול מ 25 

השתמשו במספרים שלמים

טענה 1:  נכונות : הצורה היא ריבוע

טענה 3: נכונות: הצורה היא מעויין

משימה 5

טענה 1: נכונות – התיכון במשולש העליון שווה לחצי הקולב

ציירו דלתון שהוא ריבוע

השתמשו במספרים שלמים

הקולב יותר ארוך מהשדרה 

הקולב והשדרה שווים באורכם

טענה 2 :

משולש עליון שווה צלעות

השתמשו במספרים שלמים

הקולב יותר ארוך מהשדרה 

הקולב והשדרה שווים באורכם

טענה 4:

ציירו דלתון שהוא ריבוע

השתמשו במספרים שלמים

הקולב יותר ארוך מהשדרה 

הקולב והשדרה שווים באורכם

משימה 1 

• מה צריכים להיות אורכי האלכסונים כדי לקבל שטח מפרש הכי גדול? (אלכסונים הכי ארוכים כלומר 60,60), וכדי לקבל שטח מפרש הכי קטן? (אלכסונים הכי קצרים כלומר 50,50) 
• כדאי לדון עם התלמידים במסקנה לגבי מה צריך לשנות כדי לקבל שטחים שונים? (אורכי האלכסונים)   
• האם יש חשיבות למיקום נקודת החיתוך של האלכסונים? (לא) 
• האם יש צורה מיוחדת לעפיפון שהתלמידים יצרו (ריבוע/מעויין..)?

משימה 2

• יש להדגיש לתלמידים שצריך להשתמש בשני מקלות שונים.
• כמה אפשרויות שונות יש לבניית עפיפונים העונים על הדרישה? (הרבה – כי ניתן לבנות עפיפונים עם אותו אורך של השדרה ואותו אורך של הקולב אך עם שינוי מיקום נקודת החיבור של המקלות, וגם אפשר להחליף בין המקלות ובאותו אופן לשנות את מיקום נקודת החיבור)
• האם יש צורה מיוחדת לעפיפון שהתלמידים יצרו (ריבוע/מעויין..)?

משימה 3 

• יש לדון עם התלמידים במה משותף לכל הדוגמאות הנכונות? (כל המחלקים של 1800 )
• בשונה ממשימות 1+2, במשימה זו נתון השטח של העפיפון. לכן, על מנת למצוא את אורכי האלכסונים על התלמידים למצוא את המחלקים של המספר. 
• יש להדגיש לתלמידים כי לא בהכרח מדובר על "גורמים" של המספר אלא על "המחלקים" שלו (יש להבחין בין שני מושגים אלה). 

משימה 4

• בשונה מהמשימות הקודמות, במשימה זו יש דרישות לגבי השטח וגם הצורה של העפיפון.
• גם במשימה זו נתון השטח של העפיפון, ולכן על מנת למצוא את אורכי האלכסונים על התלמידים למצוא את המחלקים של המספר. 
• מה מאפיין את אלכסוני הריבוע ? ואת אלכסוני המעויין?
• יש לדון עם התלמידים למה אי אפשר לבנות עפיפון שצורתו טרפז

משימה 5 

• טענה 1: מה צריך להתקיים כדי שלעפיפון תהיה זווית ישרה אחת בלבד? (התיכון במשולש העליון צריך להיות שווה לחצי הקולב – כלומר כאשר המשולש העליון הוא משולש ישר זווית ושווה שוקיים)
• יש לדון במקרה פרטי כאשר הדלתון הוא ריבוע.  

• טענה 2: מה צריך להתקיים כדי שלעפיפון יהיו בדיוק שתי זוויות ישרות? (החצי של הקולב בריבוע צריך להיות שווה למכפלת הקטעים של השדרה) 
• כדאי לדון בתכונות של משולש הזהב (30,60,90 בעל הזוויות)
• יש לדון במקרה פרטי כאשר המשולש העליון הוא שווה צלעות (ניתן להשתמש במשפט תאלס) 

• למה טענה 3 לא נכונה? (אין מרובע שיש בו רק 3 זוויות ישרות)

• טענה 4 : מה צריך להתקיים כדי שלעפיפון יהיה 4 זוויות ישרות? (המשולש העליון הוא משולש שווה צלעות וגם המשולש התחתון הוא שווה צלעות – כלומר העפיפון יהיה בצורת ריבוע)
• ניתן להשתמש בדמיון משולשים כדי למצוא זוויות ישרות