מטרת הפעילות היא לחזק את המיומנות האלגברית של פונקציה קווית.

הנושא של פונקציה קווית נלמד בדרך כלל בכיתות ח. הפעילות מתאימה כפעילות מסכמת בנושא של פונקציה קווית, פעילות חזרה בכיתה ט או פעילות בנושא של גיאומטריה אנליטית – קו ישר בתיכון ברמה של שלוש יחידות. לפעילות זו קיימת פעילות מקדימה אלגברה של פונקציות – פונקציה קווית – 1

• שיפוע של פונקציה קווית
• משמעות נקודות על הצירים
• גרף שעובר בנקודות נתונות
• משמעות הפרמטרים בביטויים אלגבריים של פונקציה קווית f(x)=mx+b  ו- f(x)=m(x-p)
• ביטוי אלגברי של פונקציה קווית שהגרף שלה עובר בנקודה הנתונה ומקביל לגרף אחר
• מיומנות אלגברית של טכניקות בביטויים אלגבריים

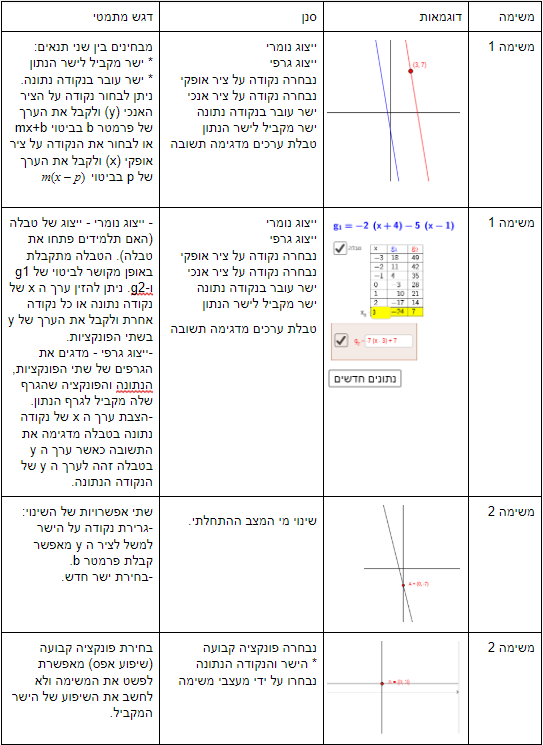
תרגיל 1: ייצוג נומרי, נבחרה נקודה על הציר האופקי, נבחרה נקודה על הציר האנכי, ייצוג גרפי

ישר אינו מקביל לישר הנתון, טבלת ערכים מדגימה תשובה

 תרגיל 2: שינוי מנתונים התחלתיים, נקודה נוחה, ייצוג נומרי, הביטוי האלגברי מתאר את הגרף

תרגיל 3 : ייצוג גרפי של פונקציית הסכום, האם נבחרה נקודה על הישר של פונקציה f,נבחרה פונקציה קבועה, טבלת ערכים מדגימה תשובה ,   g פונקציה קבועה, פונקציית סכום עוברת בנקודה, האם הפונקציה הנוספת עוברת בנקודה

הפעילות עוסקת במיומניות אלגבריות, יחד עם זאת, הגישה הפונקציונלית לאלגברה פותחת בפני תלמידים נקודות מבט נוספות למיומנוית אלה. בחירת נקודה על אחד הצירים מאפשרת שימוש בצורות שונות של ייצוג אלגברי של פונקציה קווית.

f(x)=mx+b מבליט את הפרמטר b  כנקודת חיתוך של גרף הפונקציה עם ציר ה y

f(x)=m(x-p) מבליט את הפרמטר p  כנקודת חיתוך של גרף הפונקציה עם ציר ה x

פעילות זו היא פעילות מסכמת בנושא של פונקציה קווית.

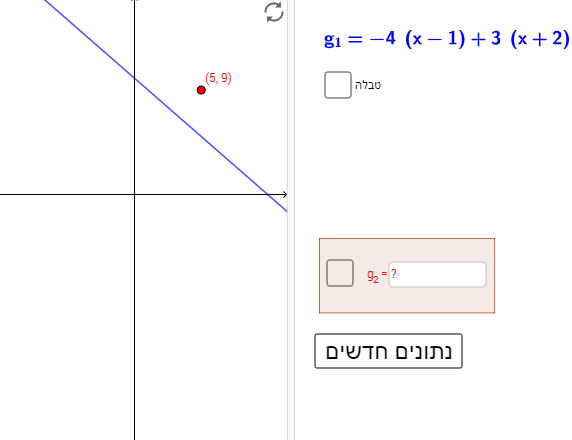
משימה 1 עוסקת בתרגול של כתיבת ביטוי אלגברי לפונקציה קווית שהגרף שלה מקביל לגרף הנתון.

משימה 2 עוסקת בכתיבת ביטוי אלגברי לפי ייצוג גרפי של פונקציה קווית ונקודה על הישר. כדאי לדון עם תלמידים על אילו תנאים מספיקים ואילו הכרחיים לכתיבת ביטוי אלגברי (שתי נקודות על מגדירות ישר באופן חד משמעי)

במשימה  3 נדרשת מהתלמידים מיומנות של טכניקה אלגברית של חוק פילוג והבנת המושג סכום של שתי פונקציות.המשימה מבוססת על החוק 

f(x)+g(x)=(f+g)(x)

נתון ביטוי אלגברי של פונקציה f ונתונה נקודה המקיימת את f+g. המטרה של המשימה למצוא את g. תלמידים מתבקשים לכתוב ביטוי אלגברי שמתאים לשני התנאים. 

נדגים את הפתרון הכללי:

נתון f(x) ו- (x0,y0)

צריך למצוא את g(x) כך ש  f(x0)+g(x0)=(f+g)(x0) או  f(x0)+g(x0)=y0

למעשה

 g(x0)=y0-f(x0)

כל פונקציה g המקיימת את התנאי הזה היא הפתרון של המשימה.

בפעילות ניתנת לתלמידים אפשרות לבחור (בעזרת כפתור "נתונים חדשים") את הנתונים למשימה. אפשר לדון עם תלמידים על אפשרויות השונות שהופיעו בשטיח של הגשות. מה הנתונים שחלק גדול מהתלמידים בחרו. מדוע? מה הנתונים שרק תלמידים בודדים בחרו? מדוע? האם יש אפשרויות נוספות שהיה כדאי לנו לבחור.