ריבועיות
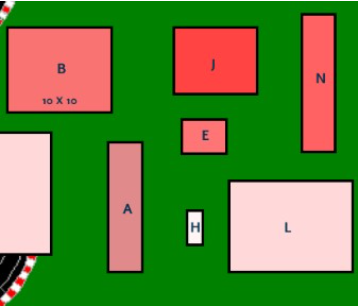
פעילות זו מבוססת על פעילות של פרופסור יהודה שוורץ ז"ל , שבה הוא מנסה לנסח מידה לריבועיות של מלבנים.
קישור לכיתת התנסות
משימה 1: סידור מלבנים לפי מידת הריבועיות שלהם
להעריך את יכולת מיון מלבנים וסידורם לפי מידת הריבועיות, מהמלבן הריבועי ביותר אל הפחות ריבועי. הרעיון כאן הוא ההתנסות בסידור מלבנים והגשת תשובה של התלמיד.
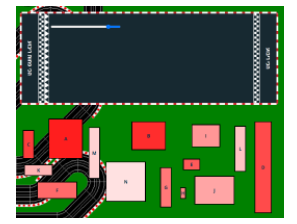
משימה 2: הצעת מידות לריבועיות של מלבנים באמצעות אורך (H) ורוחב (W)
להעריך את היכולת לנסח ביטוי/מודל למידת הריבועיות של מלבנים, באמצעות שני מימדים אורך (H) ורוחב (W). הרעיון כאן הוא שתלמידים הם אלה שקובעים מידה מתמטית, אין תשובה נכונה או לא נכונה, המטרה היא לדון במה יותר מתאים לדוגמאות שהתלמיד נותן.
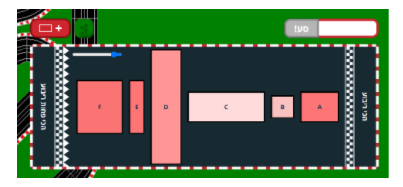
משימה 3: השוואה בין מידות שונות של ריבועיות
להעריך את היכולת להשוות בין מידות נתונות של ריבועיות והיכולת לזהות דוגמאות למלבנים שונים שיש להם אותה מידה של ריבועיות לפי ביטויים/מודלים שונים.
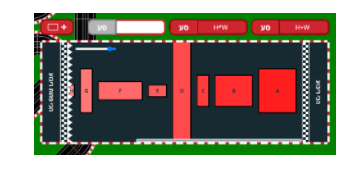
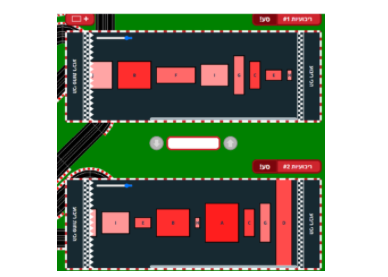
משימה 4: גילוי המודלים לפיהם מסודרות שתי סדרות של מלבנים
להעריך את היכולת לפענח את המודלים שבאמצעותם סודרו שתי סדרות של מלבנים.
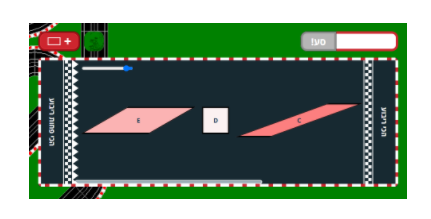
משימה 5: מידה לריבועיות של מקביליות
להעריך את היכולת לנסח ביטוי/מודל למידת הריבועיות של מקבילית, באמצעות 3 מימדים (אורך, רוחב וזווית בסיס).
"החשיבות בהרחבה הוא לא במספר הפרמטרים במודל המוצע, אלא בהזדמנות לתת לתלמידים שאין להם ידע רב מאוד במתמטיקה ל"עשות מתמטיקה" חדשה. זכות זאת שמורה בדרך כלל רק למתמטיקאים ועובדה זו נותנת תמונה מסולפת של המתמטיקה." מתוך חוברת הערכה מאוזנת – פרופ' יהודה שוורץ ז"ל.
התלמידים נחשפים לנושא המרובעים בבית ספר יסודי כאשר הם לומדים את משפחת המרובעים ובפרט את התכונות המאפיינות כל אחד מהמרובעים: ריבוע, מלבן, דלתון, מקבילית, טרפז.
בחט"ב, התלמידים לומדים דרכים לזיהוי מרובע מסויים מכלל המרובעים, ואת היחסים ההדדיים בין קבוצות שונות של מרובעים (קשרי הכלה, קשרי זרות, וקשרי חפיפה חלקית). כמו כן, בתחילת כיתה ז' התלמידים לומדים איך לנסח ביטויים והצבת מספרים בהם, ובכיתה ח' הם לומדים את נושא היחס והפרופורציה. כל הנושאים האלה חשובים להתמודדות עם פעילות הריבועיות, לכן השלב המתאים להעברת הפעילות הוא אמצע כיתה ח' עד כיתה י'.
ניתן להעביר את הפעילות כפעילות פתיחה לנושא "מידה", או כתרגול וחזרה על נושא "מרובעים".
- הכרת מושגים בסיסיים בגאומטריה: צלע, זווית, סוגי זוויות, מרובע, אורך ורוחב.
- הכרת הגדרות של הריבוע, המלבן והמקבילית: הגדרה, תכונות, ותנאים מספיקים לקבלה.
- היכולת לנסח ביטויים ולהציב בהם
- יחס ופרופורציה
משימה 1:
דוגמה 1: התלמיד סידר את הריבוע (מלבן N) כראשון מצד ימין בסדרה.
המלבנים B, I, E, H, A (ההפרש בין אורכי הצעות הוא 1) סודרו אחד ליד השני מצד שמאל לריבוע N, ואז סידר את שאר המלבנים לפי הסדר הזה: D, M , L, G, F כלומר התלמיד הסתכל על ההפרש בין הצלעות (ככל שההפרש גדול יותר אז המלבן יופיע בצד שמאל יותר).
משימה 2:
נסמן באות H את האורך של המלבן, ובאות W את הרוחב שלו.
דוגמה 1: התלמיד הגיש את היחס H/W כמידה לריבועיות.
צריך להדגיש לתלמיד שבמקרה זה יהיה שוני בין מלבן במידות 6×3 לעומת מלבן במידות 3×6.
דוגמה 2: התלמיד הגיש את W/H+H/W כמידה לריבועיות.
צריך להדגיש לתלמיד שבמקרה זה מידת הריבועיות של ריבוע תמיד תהיה 2.
דוגמה 3:
התלמיד הגיש את 0.5*(W/H+H/W) כמידה לריבועיות.
דוגמה 4:
התלמיד הגיש את 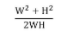 כמידה לריבועיות, שזה בעצם הפשטה לביטוי שהופיע בדוגמה 3.
כמידה לריבועיות, שזה בעצם הפשטה לביטוי שהופיע בדוגמה 3.
במקרה זה, התלמיד יצר מדד ע"י השוואה בין שני שטחים.
דוגמה 5:
התלמיד הגיש את ![]() כמידה לריבועיות. במקרה זה, התלמיד יצר מדד ע"י הסתכלות על שטח הריבוע הבנוי על הצלע W ועל שטח הריבוע הבנוי על הצלע H.
כמידה לריבועיות. במקרה זה, התלמיד יצר מדד ע"י הסתכלות על שטח הריבוע הבנוי על הצלע W ועל שטח הריבוע הבנוי על הצלע H.
צריך להדגיש לתלמיד שבמקרה זה מידת הריבועיות של מלבנים דומים תהיה שונה.
דוגמה 6:
התלמיד הגיש את 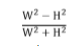 כמידה לריבועיות. יחס זה הינו גם כן יחס של שני שטחים.
כמידה לריבועיות. יחס זה הינו גם כן יחס של שני שטחים.
דוגמה 7:
התלמיד הגיש את W-H כמידה לריבועיות.
צריך להדגיש לתלמיד שבמקרה זה שני מלבנים עם מידות שוות יהיו עם מידת ריבועיות שונה.
למשל מלבן 6×4 ומלבן 4×6 .
דוגמה 8:
התלמיד הגיש את |W-H| כמידה לריבועיות.
במקרה זה, שני מלבנים דומים יהיו עם מידת ריבועיות שונה.
למשל מלבן 2×6 (מידת הריבועיות היא 4) ומלבן 6×18 (מידת הריבועיות היא 12) .
וגם אם נמדוד את המלבן במ"מ ולא בס"מ, אזי למלבן הראשון תהיה מידת ריבועיות 40 מ"מ ולשני 120 מ"מ. לכן צריך שתהיה מידת ריבועיות בלתי תלויה ביחידות אורך.
דוגמה 9:
התלמיד הגיש את 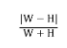 כמידה לריבועיות. במקרה זה, מידת הריבועיות של הריבוע תהיה 0 ואילו של מלבן ארוך ונמוך או מלבן צר וגבוה תהיה 1.
כמידה לריבועיות. במקרה זה, מידת הריבועיות של הריבוע תהיה 0 ואילו של מלבן ארוך ונמוך או מלבן צר וגבוה תהיה 1.
דוגמה 10:
התלמיד הגיש את 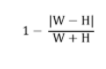 כמידה לריבועיות.
כמידה לריבועיות.
- המלבן N הוא הראשון מצד ימין.
- שימוש בפעולה חשבונית אחת.
- שימוש ביותר מפעולה חשבונית אחת.
- קיימים שני מלבנים במנחים שונים ומידת הריבועיות שלהם שונה.
- קיימים שני מלבנים דומים ומידת הריבועיות שלהם שונה.
- מידת הריבועיות של הריבוע שווה לאפס
- מידת הריבועיות של הריבוע שווה לאחד
בדיון הכיתתי חשוב להסתכל על כל דוגמאות שמקיימות את מידת הריבועיות שהוצעה ולחשוב מה הגורמים המשפיעים לכך.
על כל מידה שהתלמידים מציעים, לשאול את השאלות הבאות:
- מה היא מידת הריבועיות של הריבוע לפי המידה שהוצעה?
- מה קורה למידת הריבועיות שהוצעה כאשר הופכים מידות רוחב ואורך של המלבן?
- מה קורה למידת הריבועיות של שני מלבנים דומים?
שאלות לדיון למשימה 5:
- האם מקבילית שכל צלעותיה שוות היא ריבוע? – לא בהכרח – דוגמה נגדית: מעוין
- האם מקבילית שכל זוויותיה ישרות היא ריבוע? – לא בהכרח – דוגמה נגדית: מלבן
- האם מקבילית שכל צלעותיה שוות וכל זוויותיה ישרות היא ריבוע?
- חשבו על פרמטרים אחרים שניתן באמצעותם להגדיר את מידת הריבועיות של מקבילית? (התייחסות לאלכסונים, ליחס בין זוויות סמוכות, לגובה המקבילית וכד')







