המטרה הכללית של הפעילות היא להעריך אם התלמידים מבינים תכונות של פונקציה ריבועית, ויודעים להשתמש בהן כדי למצוא דוגמאות לשדות עם תנאים שונים.

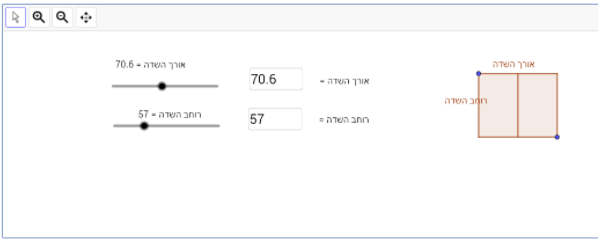
ועד המושב חילק לכל החקלאים במושב גדר רשת חשמלית יקרה באורך 210 מטרים.

החקלאים התבקשו ליצור בעזרת הגדר שדה מלבני המחולק לשתי חלקות מלבניות שוות שטח ובכל חלקה לגדל גידול שונה שיבחרו.

כדי למנוע בזבוז של גדר יקרה, ועד המושב קבע שכל חקלאי חייב להשתמש בכל גדר הרשת החשמלית שקיבל לגידור השדה וליצירת הגדר המפרידה בין שתי החלקות.

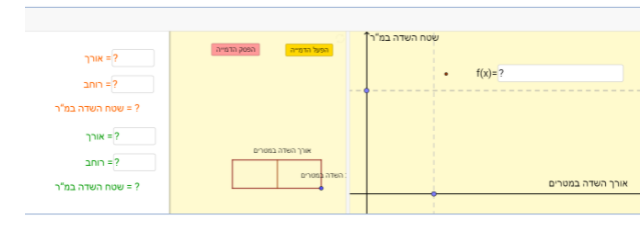
 המשימה הראשונה  היא משימה מקדימה, שבה התלמיד מתבקש להגיש שלוש דוגמאות של שדות מלבניים שונים שאפשר ליצור באמצעות גדר הרשת החשמלית שהחקלאים קיבלו והעונים על דרישות ועד המושב.

חשוב לחדד לתלמידים כך שצריך להשתמש בכל גדר הרשת גם לגידור החיצוני וגם לגדר המפרידה בין שתי החלקות. 

המטרה של משימה זו היא להבין את הקשר בין האורך השלם של הגדר החשמלי לבין מידות השדה, תוך התחשבות בזה שיש מחיצה בין שתי החלקות.

במשימה השנייה נתון כי אחד החקלאים תכנן שדה שעונה על דרישות ועד המושב, שאורכו 75 מטרים ורוחבו 20 מטרים (השדה בצבע כתום).

השכן שלו אמר שהוא יכול ליצור על השטח שיש לו רק שדות שאורכם קטן מ- 75 מטרים.

 התלמיד מתבקש לכתוב ביטוי אלגברי לפונקציה (m(x המתארת את הרוחב של שדה המקיים את דרישות ועד המושב בהתאם לאורכו (x). ולאחר מכן, להגיש 3 הצעות שונות לשדות שעונים על דרישות ועד המושב ושהשכן יכול ליצור.

כדי ליצור שדות כאלה התלמיד מתבקש לכתוב ערכים מתאימים למידות של השדה הירוק.

המטרה של משימה זו היא למצוא את הקשר בין אורך לרוחב, ולהבין שהאורך יכול להיות שווה לרוחב ויכול להיות גם קצר יותר מהרוחב. 

מטרה נוספת היא לכתוב ביטוי אלגברי המתאר את הקשר בין האורך לרוחב, כהכנה למשימה הבאה שבה צריך לכתוב ביטוי אלגברי המתאר את השטח בהתאם לאורכו של השדה.

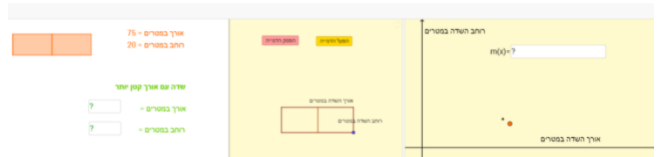
שימו לב שישנם כלים שונים המסייעים לתלמידים לחקור ולבדוק את התשובות שלהם, כך שבחלון הימני ביישומון התלמיד יכול להציג גרף המתאר את רוחב השדה בהתאם לאורכו, ע"י לחיצה על "הפעל הדמייה" או גרירת הנקודה הכחולה בסרטוט של השדה.

(הערה: הזזה של מערכת הצירים תאפס את ההדמייה).

בנוסף, הנקודה הכתומה שמופיעה במערכת הצירים מייצגת את רוחב השדה שאורכו 75 מטר.

עם הכנסת ערכים למידות של השדה הירוק, תוצג במערכת הצירים נקודה ירוקה המייצגת את רוחב השדה הירוק בהתאם לאורכו.

במשימה השלישית, נתון שיוסי החקלאי יצר שדה שאורכו 21 מטר שעונה על הדרישות שקבע ועד המושב (שדה בצבע כתום). רוחב השדה שלו הוא 56 מ' ושטחו 1176 מ"ר.

שטח השדה שהתקבל נראה ליוסי גדול מדי והוא רצה לתכנן שדה ששטחו קטן יותר שגם הוא מתאים לדרישות של ועד המושב.

התלמיד מתבקש לכתוב ביטוי אלגברי לפונקציה (f(x המתארת את השטח של השדה בהתאם לאורכו. ולאחר מכן, להגיש 3 הצעות שונות לשדות שעונים על דרישות ועד המושב וששטח כל אחד מהם הוא קטן מ- 1176 מ"ר. כדי ליצור שדות כאלה, על התלמיד לכתוב ערכים מתאימים למידות של השדה הירוק.

המטרה של המשימה הזו היא להבין את הקשר בין אורך השדה לשטח שלו, תוך שימוש בביטוי האלגברי שהתקבל במשימה הקודמת, ולמצוא את השדה עם שטח קטן יותר משטח השדה הנתון.

כמו כן, מטרה נוספת היא להבין את הקשר בין הייצוגים השונים: בין הגרף והנקודות המתקבלות במערכת הצירים לבין התיאור המילולי. 

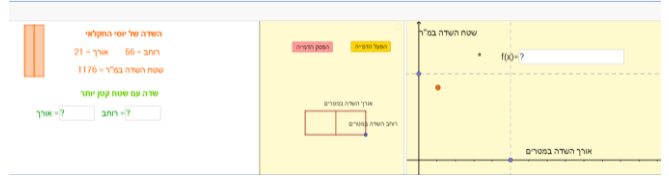
בחלון הימני ביישומון תוכלו להציג גרף המתאר את שטח השדה בהתאם לאורכו, ע"י לחיצה על "הפעל הדמייה" או גרירת הנקודה הכחולה בסרטוט של השדה.

(הערה: הזזה של מערכת הצירים תאפס את ההדמייה).

הנקודה הכתומה שמופיעה במערכת הצירים מייצגת שטח השדה של החקלאי (שאורכו 21 מטר).

עם הכנסת ערכים למידות של השדה הירוק, תוצג במערכת הצירים נקודה ירוקה המייצגת את שטח השדה הירוק בהתאם לאורכו.

במשימה הרביעית, נתון כי חקלאי רצה ליצור שדה ששטחו גדול ככל האפשר וגם עונה על הדרישות של ועד המושב.

הוא קיבל 3 הצעות מחברים לשדות שאפשר ליצור:

הצעה א: שדה שצורתו ריבוע

הצעה ב : שדה מלבני המחולק לשתי חלקות ריבועיות.

הצעה ג: שדה ששטחו 1837.5 מ"ר.

נתונות 3 טענות של החקלאי.

התלמיד מתבקש לסמן  את הטענות הנכונות, ולכל טענה נכונה להגיש דוגמה תומכתע"י הכנסת ערכים מתאימים למידות של השדה בהצעה (השדה הכתום) וערכים מתאימים למידות של שדה ששטחו גדול יותר מהשדה בהצעה (השדה הירוק).

הטענות של החקלאי:

• אפשר ליצור שדה ששטחו גדול יותר מהשדה בהצעה א
• אפשר ליצור שדה ששטחו גדול יותר מהשדה שבהצעה ב
• אפשר ליצור שדה ששטחו גדול יותר מהשדה שבהצעה ג

בדרך כלל בהינתן היקף של מלבן (בלי מחיצה), השטח הגדול ביותר מתקבל כשהמלבן הוא ריבוע. כלומר רוב התלמידים יודעים שריבוע הוא המלבן בעל השטח המקסימלי, אבל זה לא נכון במקרה הנתון כשיש מחיצה באמצע.

לכן, המטרה של המשימה הזו היא לתת לתלמידים להתמודד עם התפיסה השגויה הזו ולמצוא דוגמאות של מלבנים עם מחיצה שיש להם שטח גדול יותר משל הריבוע. 

בנוסף, המטרה של טענה 3 היא לגרום לתלמיד לחפש את השטח המקסימלי ואז להבין שכל מה שגדול ממנו לא נמצא על הפונקציה (כלומר לא מקיים את הדרישות של הועד).

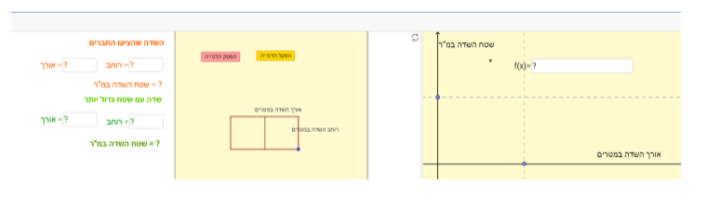
במשימה החמישית,  נתון כי רונית ודנה החקלאיות במושב רוצות ליצור שדות בעלי אותו השטח המתאימים לדרישות של ועד המושב.

כמו כן, נתונות טענות.

התלמיד מתבקש לבחור את הטענות הנכונות, ולכל טענה נכונה להגיש דוגמה תומכת של שדה של רונית (שדה כתום) ושדה של דנה (שדה ירוק).

1. ניתן לתכנן שני שדות השווים בשטחם ושונים במידותיהם.
2. ניתן לתכנן יותר משני שדות השווים בשטחם ושונים במידותיהם.
3. ניתן לתכנן שדה כך שלא קיים שדה שונה במידותיו ושווה לו בשטחו.

המטרה של המשימה הזו היא להבין שהפונקציה הריבועית היא סימטרית ולהשתמש בתכונת הסימטריה, כלומר להבין שלכל נקודה (חוץ מהמקסימום) יש נקודה סימטרית: ערכי ה-X שונים אך ערכי ה-Y שווים.

במשימה השישית, נתונות טענות שהעלה יעקוב החקלאי לגבי שדות המקיימים את דרישות ועד המושב.

התלמיד מתבקש להגיש לכל טענה דוגמה תומכת.

הטענות:

 1) קיימים שני שדות שונים במידותיהם כך שההיקף של הראשון (הכתום) גדול מההיקף של השני (הירוק) והשטח של הראשון גם הוא גדול מהשני.

2) קיימים שני שדות שונים במידותיהם כך שההיקף של הראשון (הכתום) גדול מההיקף של השני (הירוק) והשטח של הראשון קטן מהשטח מהשני

3) קיימים שני שדות שונים במידותיהם כך שההיקף של הראשון (הכתום) גדול מההיקף של השני (הירוק) והשטח של הראשון שווה לשטח של השני

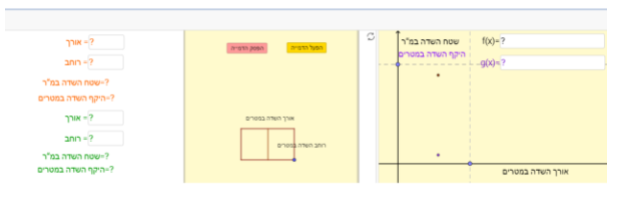
המטרה של המשימה הזו היא להבין את הקשר בין היקף השדה לשטחו, להבין את הקשר בין פונקציה ריבועית לפונקציה קווית ולמצוא מצבים הדדיים שונים לפי התנאים הנתונים.

בחלון הגרפי בצד ימין, התלמיד יכול להציג שני גרפים: גרף המתאר את שטח השדה בהתאם לאורכו (הגרף החום) וגרף המתאר את היקף השדה בהתאם לאורכו (הגרף הסגול), ע"י לחיצה על "הפעל הדמייה" או גרירת הנקודה הכחולה בסרטוט של השדה (הערה: הזזה של מערכת הצירים תאפס את ההדמייה).

כמו כן, התלמיד יכול לכתוב ביטוי אלגברי (f(x המתאר את שטח השדה בהתאם לאורכו וביטוי (g(x המתאר את היקף השדה בהתאם לאורכו.

עם הכנסת ערכים למידות של השדות תוצג במערכת הצירים שתי נקודות ירוקות: אחת מתאימה להיקף השדה הירוק שהצגתם והשנייה לשטח השדה הירוק, ותוצג גם שתי נקודות כתומות: אחת מתאימה להיקף השדה הכתום שהצגתם והשניה לשטח השדה הכתום.

הפעילות משלבת בין תכונות של פונקציה ריבועית לנושא שטח והיקף של מלבן, והיא כוללת פתרון של בעיית קיצון של פונקציה ריבועית. לכן, הפעילות מתאימה לתלמידי כיתה ח' עד י' אשר למדו את נושא הפונקציה הריבועית.

כמו כן, ניתן להעביר את הפעילות כלימוד נושא פתרון בעיית קיצון בעזרת תכונות של פונקציה ריבועית. 

המושגים "היקף" ו'שטח" נלמדים בבית הספר היסודי וגם בכיתה ז', כך שלפי תוכנית הלימודים "יש לעסוק בשטח של מלבן באמצעים מספריים ואלגבריים ולהדגיש את ההשתנות בשטח המלבן כתוצאה משינוי באורכי הצלעות". (ראה עמוד  18   בתוכנית הלימודים של חט"ב)

נושא כתיבת ביטויים אלגבריים נלמד בכיתה ז' הכולל הכללה של תופעות מספריות, הצבה בביטוי אלגברי ופתרון משוואות עם משתנה אחד. (ראה עמוד  5   בתוכנית הלימודים של חט"ב)

נושא תכונות של פונקציה ריבועית נלמד בכיתה ט' והוא כולל הסימטריות, קודוד הפרבולה, פתרון באמצעים אלגבריים וגרפיים, ותחומי ירידה ועלייה של הפונקציה הריבועית. (ראה עמוד  108   בתוכנית הלימודים של חט"ב)

היקף ושטח מלבן

כתיבת ביטויים אלגבריים

תכונות של פונקציה ריבועית

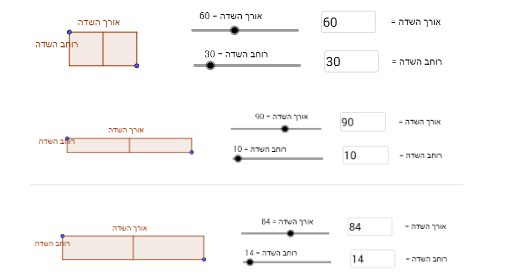
משימה 1:

על מנת לקבל תשובה נכונה, צריך שיתקיים 210 = 2*האורך + 3*הרוחב .

למשל:

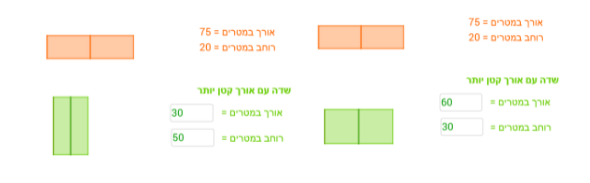
משימה 2:

על מנת לקבל תשובה נכונה, צריך שתתקיים הדרישה של ועד המושב ( 210 = 2*האורך + 3*הרוחב ), וגם לכתוב ערכים למידות שדה עם אורך קטן יותר.

למשל:

כמו כן, הביטוי האלגברי המתאים לפונקציה (m(x המתארת את הרוחב של שדה בהתאם לאורכו (x) הוא כל ביטוי השקול ל: 

(210 – 2x) / 3

משימה 3 :

הביטוי האלגברי המתאים לפונקציה (f(x המתארת את השטח של השדה בהתאם לאורכו הוא כל ביטוי השקול ל: 

[x (210 – 2x)] / 3

על מנת לקבל תשובה נכונה, צריך שאורך השדה יהיה קטן מ- 21 או גדול מ- 84 (בנוסף שתתקיים הדרישה של ועד המושב)

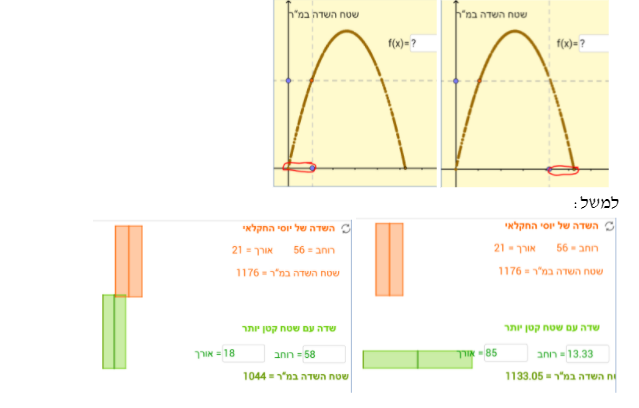
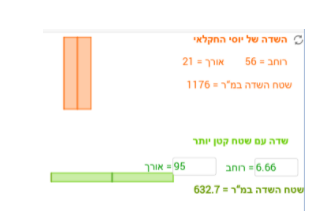
משימה  4:

טענה 1 נכונה – אפשר ליצור שדה ששטחו גדול יותר משטח השדה הריבועי, וגם עונה על הדרישות של ועד המושב

טענה 2 נכונה – אפשר ליצור שדה ששטחו גדול יותר משטח השדה שכל חלקה בו היא ריבועית, וגם עונה על הדרישות של ועד המושב

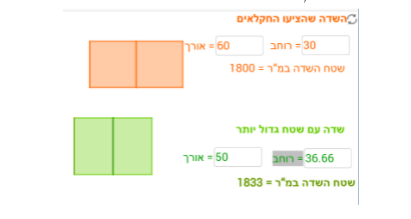
טענה 3 לא נכונה, כלומר אין שדה שיש לו שטח יותר גדול מ- 1837.5 מ"ר.

משימה 5:

טענה 1 נכונה. דוגמה תומכת: 

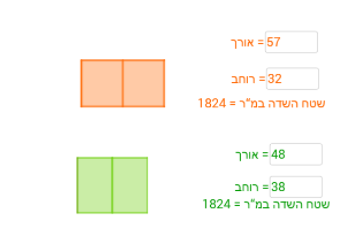
טענה 2 לא נכונה. לא ניתן לתכנן יותר משני שדות השווים בשטחם ושונים במידותיהם.

טענה 3  נכונה. דוגמה תומכת: 

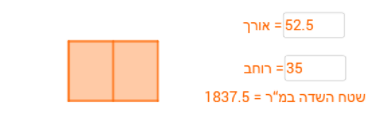
משימה  6:

דוגמה תומכת בטענה 1: כל שדה עם אורך שהוא קטן מערך ה- X של המקסימום, כלומר כל שדה עם אורך שהוא קטן מ- 52.5 מטר. 

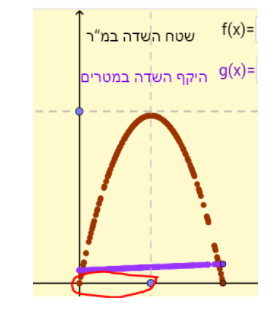
דוגמה תומכת בטענה 2: כל שדה עם אורך שהוא גדול מערך ה- X של המקסימום, כלומר כל שדה עם אורך שהוא גדול מ- 52.5 מטר. 

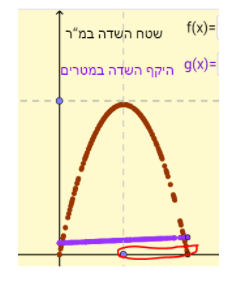
דוגמה תומכת בטענה 3: כל שתי נקודות שהן סימטריות על הגרף אבל הנקודה הכתומה היא הימנית (כלומר האורך של השדה הכתום הוא גדול יותר). 

למשל:

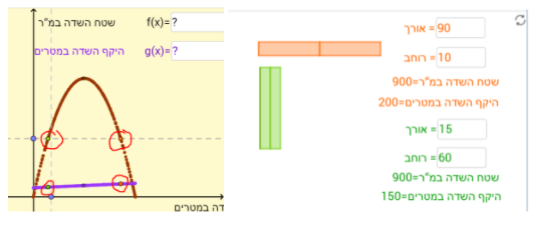
משימה 1:

השדה עונה על דרישות הועד

השדה הוא שדה ריבועי

כל חלקה בשדה היא ריבועית

נכתבו שני ערכים לא שלמים

 משימה 2 :

הוגש שדה מתאים לדרישות

השדה עונה על דרישות הועד

האורך של השדה קטן מ- 75 מטר

הרוחב של השדה גדול מהאורך שלו

הוכנסו מספרים שלמים

השדה הוא שדה ריבועי

כל חלקה בשדה היא ריבועית

משימה 3:

הוגש שדה מתאים לדרישות

השדה עונה על הדרישות של הועד

שטח השדה המוצע קטן יותר משטח השדה של יוסי

אורך השדה המוצע גדול יותר מאורך השדה של יוסי

נכתבו מספרים שלמים

השדה הוא שדה ריבועי

כל חלקה בשדה היא ריבועית

כתבו ביטוי אלגברי

השתמשו בהדמיה

משימה 4: 

טענה 1: 

נבחרה טענה 1

הוגשה דוגמה מתאימה לטענה 1

הכניסו בשדה הכתום ערכים של שדה ריבועי

הכניסו בשדה הירוק ערכים של שדה בעל שטח גדול יותר

כל חלקה בשדה הכתום היא ריבועית

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

כתבו ביטוי אלגברי

השתמשו בהדמיה 

טענה 2:

נבחרה טענה 2

הוגשה דוגמה מתאימה לטענה 2

כל חלקה בשדה הכתום היא ריבועית

הכניסו בשדה הירוק ערכים של שדה בעל שטח גדול יותר

הכניסו בשדה הכתום ערכים של שדה ריבועי

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

כתבו ביטוי אלגברי

השתמשו בהדמיה 

טענה 3: 

נבחרה טענה 3

שטח השדה הכתום הוא 1837.5 מ"ר

הכניסו בשדה הירוק ערכים של שדה בעל שטח גדול יותר

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

כתבו ביטוי אלגברי

השתמשו בהדמיה

משימה 5: 

טענה 1:

נבחרה טענה 1

הוגשה דוגמה מתאימה לטענה 1

שני השדות שווים בשטחם

שני השדות שונים במידותיהם

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

הכניסו בשדה הכתום ערכים של שדה ריבועי

הכניסו בשדה הירוק ערכים של שדה ריבועי

כתבו ביטוי אלגברי

השתמשו בהדמיה

טענה 2:

נבחרה טענה 2

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

הכניסו בשדה הכתום ערכים של שדה ריבועי

הכניסו בשדה הירוק ערכים של שדה ריבועי

כתבו ביטוי אלגברי

השתמשו בהדמיה 

טענה 3: 

בחרה טענה 3

הוגשה דוגמה מתאימה לטענה 3

הוגש שדה כתום שלא קיים שדה ששווה לו בשטחו

הוכנס ערך מקורב לאורך המקיים את הטענה

האנך נמצא על נקודת המקסימום

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

הכניסו בשדה הכתום ערכים של שדה ריבועי

הכניסו בשדה הירוק ערכים של שדה ריבועי

כתבו ביטוי אלגברי

השתמשו בהדמיה 

משימה 6: 

טענה 1:

 הוגשו שני שדות המקיימים את טענה 1

ההיקף של הראשון גדול מההיקף של השני

השטח של הראשון גדול מהשטח של השני

לאחד השדות יש את השטח המקסימלי

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

הכניסו בשדה הכתום ערכים של שדה ריבועי

הכניסו בשדה הירוק ערכים של שדה ריבועי

כתבו ביטויים אלגבריים לפונקציות

השתמשו בהדמייה

טענה 2 : 

הוגשו שני שדות המקיימים את טענה 2

ההיקף של הראשון גדול מההיקף של השני

השטח של הראשון קטן מהשטח מהשני

לאחד השדות יש את השטח המקסימלי

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

הכניסו בשדה הכתום ערכים של שדה ריבועי

הכניסו בשדה הירוק ערכים של שדה ריבועי

כתבו ביטויים אלגבריים לפונקציות

השתמשו בהדמייה

טענה 3: 

הוגשו שני שדות המקיימים את טענה 3

ההיקף של הראשון גדול מההיקף של השני

השטח של הראשון שווה לשטח של השני

האנך נמצא על נקודת המקסימום

השדה הכתום עונה על דרישות הועד

השדה הירוק עונה על דרישות הועד

הכניסו בשדה הכתום ערכים של שדה ריבועי

הכניסו בשדה הירוק ערכים של שדה ריבועי

כתבו ביטויים אלגבריים לפונקציות

השתמשו בהדמייה

משימה 1:

• חשוב לוודא שהתלמידים מבינים את הדרישה להשתמש בכל גדר הרשת גם לגידור החיצוני וגם לגדר המפרידה בין שתי החלקות. 
• יש לדון בקשר בין האורך השלם של הגדר החשמלי לבין מידות השדה, תוך התחשבות בזה שיש מחיצה בין שתי החלקות. 

משימה 2:

• יש לדון בקשר בין אורך השדה לרוחבו.
• חשוב להדגיש ולהסביר לתלמידים שהאורך של המלבן יכול להיות שווה לרוחב ויכול להיות גם קצר יותר מהרוחב. כלומר ש"אורך" לא בהכרח הצלע הגדולה ביותר במלבן.
• יש לדון בביטויים האלגבריים השונים המתארים את הקשר בין האורך לרוחב שהתלמידים הציעו.

סרטון הדגמת דיון למשימה 2:

הדגמת דיון משימה 2

משימה 3:

• יש לדון בקשר בין אורך השדה לשטח שלו.
• האם הגרף שהתקבל מהביטוי האלגברי מתלכד עם הגרף שמתקבל מהסימולציה? 
• יש לדון בביטויים האלגבריים השונים המתארים את הקשר בין האורך לשטח שהתלמידים הציעו.
• האם תלמידים השתמשו בביטוי האלגברי שהתקבל במשימה הקודמת (המתאר את הקשר בין האורך לרוחב השדה)?
• האם השדות שהתלמידים הציעו עונים על שני התנאים הנתונים: עונה על דרישות הועד וגם בעל שטח קטן יותר משטח השדה הנתון?
• יש לדון בקשר בין הייצוגים השונים: בין הגרף המתקבל מהסימולציה והנקודות המתקבלות במערכת הצירים לבין התיאור המילולי. כלומר יש לוודא שהתלמידים מבינים שהנקודות הכתומה והירוקה מתקבלות כתוצאה מהערכים שהם כתבו במידות השדה, ושנקודות אלה צריכות להיות על הגרף המתקבל מהסימולציה. 

סרטון הדגמת דיון למשימה 3:

הדגמת דיון משימה 3

משימה 4:

• לגבי טענה 1+2: יש להדגיש את הנתון שיש מחיצה באמצע השדה ולדון בתפיסה השגויה שהשטח הגדול ביותר מתקבל כשהמלבן הוא ריבוע (בדרך כלל בהינתן היקף של מלבן (בלי מחיצה), השטח הגדול ביותר מתקבל כשהמלבן הוא ריבוע. כלומר רוב התלמידים יודעים שריבוע הוא המלבן בעל השטח המקסימלי, אבל זה לא נכון במקרה הנתון כשיש מחיצה באמצע).
• לגבי טענה 3: כדי להפריך טענה זו, צריך למצוא את השטח המקסימלי לפי הגרף ולראות שזה השטח הנתון לכן אין שדה שיש לו שטח גדול יותר ועונה על התנאים. 
• על מנת למצוא את השטח המקסימלי, יש לדון עם התלמידים לגבי השלבים הבאים: יש להבין שהטווח של אורך השדה נע בין 0 ל 210 (האורך של גדר הרשת החשמלית), ולכן הערך האמצעי של אורך השדה הוא 52.5 שבו מתקבל השטח המקסימלי (לפי תכונת הסימטריות של הגרף). לאחר מכן צריך לחשב את הרוחב, לכתוב את הערך ואז ייחושב השטח באופן אוטומטי (שהוא 1837.5 מ"ר).

סרטון הדגמת דיון למשימה 4:

הדגמת דיון משימה 4

משימה 5: 

• יש לדון בתכונות הפונקציה הריבועית ובפרט בסימטריות שלה, כלומר להבין שלכל נקודה (חוץ מהמקסימום) יש נקודה סימטרית: ערך ה-X שונה אך ערך ה-Y שווה.
• יש לשים לב לדוגמאות של התלמידים לטענה 3, במקרה ונכתב ערך מקורב לאורך המקיים את הטענה (כלומר אחד הערכים 51, 52, 53, 54)  זה יכול להעיד שהתלמיד קרא את המקסימום בגרף אבל לא ידע איך לחשב אותו בדיוק. 

משימה 6:

• האם תלמידים נעזרו בכתיבת ביטויים אלגבריים המתארים את השטח בהתאם לאורך ואת ההיקף בהתאם לאורך?
• יש לדון בקשר בין היקף השדה לשטחו, כלומר לדון בקשר בין פונקציה ריבועית לפונקציה קווית.
• יש לסכם ולדון במצבים ההדדיים השונים בין פונקציה ריבועית לפונקציה קווית עולה.