הקדמה:

במושב החליטו לחלק את השטח החקלאי לתושבים בצורה הבאה: כל תושב קיבל גדר רשת באורך 240 מטרים שבאמצעותו הוא יכול לגדר לעצמו שדה מלבני.

חלק מהתושבים בחרו לגדל גידול אחד בשדה שלהם וחלק אחר החליטו לפזר סיכונים ולגדל גידולים שונים בשדה.

לפי תקנות ועד המושב, אם תושב בחר לגדל בשדה יותר מגידול אחד אז עליו להשתמש בכל גדר הרשת שקיבל לגידור השדה וגם ליצירת המחיצות בין החלקות. על כל המחיצות לצאת מאותה צלע ולהיות מאונכות לצלע הנגדית. הצלע שממנה יוצאים המחיצות תכונה "צלע המחיצות".

משימה 1

אחרי שהתושבים במושב בחרו את מספר הגידולים שהם רוצים לגדל, חלק מהם רצו ששטח השדה שלהם יהיה גדול ככל האפשר.

הגישו 3 דוגמאות של חלוקות שונות של שדות כאלה שהתושבים יכלו לגדר. 

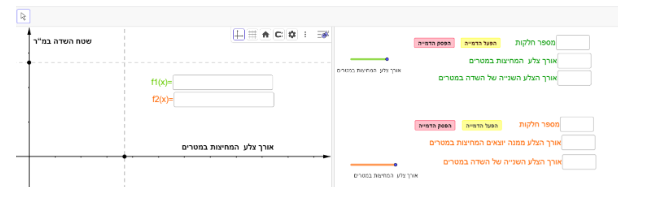
ביישומון הדינאמי עליכם לקבוע תחילה את מספר החלקות בשדה. 

לאחר מכן, תוכלו לגרור את הנקודה האדומה בקצה צלע המחיצות ולקבל גרף המתאר את שטח השדה בהתאם לאורך צלע זו. תוכלו להיעזר בגרף זה כדי לקבוע את מידות השדה בדוגמה שלכם.

בכל דוגמה כתבו בחלון הימני ביישומון את מידות השדה המלבני שיצרתם. לאחר שכתבתם את מידות הצלעות  תופיע בחלון הגרפי  נקודה בצבע ירוק המתארת את שטח השדה שיצרתם בהתאם לאורך צלע המחיצות בשדה שלכם. תוכלו להיעזר בנקודה זו לבדוק אם מידות השדה שהצעתם מתאימים.

בחלון הגרפי בצד שמאל, התלמיד יכול לכתוב ביטוי אלגברי (f(x המתאר את שטח השדה בהתאם לאורך צלע המחיצות.

משימה 2

נתונות טענות.

סמנו את הטענות הנכונות, ולכל טענה נכונה הגישו דוגמה תומכת של שני שדות שמתאימים לטענה.

הטענות:

1. אם תושב בחר לגדל יותר גידולים מהשכן שלו, אז שטח השדה שלו יהיה בהכרח קטן משטח השדה של השכן שלו.
2. אם תושב בחר לגדל יותר גידולים מהשכן שלו, אז השטח הגדול ביותר שיוכל לגדר יהיה בהכרח קטן מהשטח הגדול ביותר שיוכל לגדר השכן שלו.
3. אם תושב בחר לגדל יותר גידולים מהשכן שלו, ולו ולשכנו יש שדות עם צלע אחת שווה באורכה שטח השדה שלו יכול להיות גדול מזה של השכן שלו.
4. אם תושב בחר לגדל יותר גידולים מהשכן שלו ושניהם בחרו לגדר שדה גדול ככל האפשר אז לשדות שלהם בהכרח תהיה צלע אחת באורך 60 מ.

משימה 3

שני תושבים שבחרו לגדל מספר שונה של גידולים בשדה שלהם התעקשו לגדר שדה ששטחו גדול ככל האפשר.

טענה: קיימת אפשרות ששטח השדה של אחד מהתושבים האלה גדול  פי 2 משטח השדה של תושב אחר כזה.

אם הטענה נכונה הגישו 3 דוגמאות של זוגות תושבים כאלה אשר תומכים בטענה.

אם הטענה אינה נכונה הסבירו.

משימה 4 

חלק מהתושבים התעקשו לגדל יותר מגידול אחד ולגדר שדה גדול ככל האפשר במסגרת מספר הגידולים שבחרו לגדל.

נתונות שתי טענות. בחרו את הטענות הנכונות ולכל טענה הגישו דוגמה תומכת.

1. בקרב התושבים האלה קיימת אפשרות שהיחס בין שטח השדה של אחד התושבים לשטח השדה של תושב אחר הוא 2:3
2. בקרב התושבים האלה קיימת אפשרות שהיחס בין שטח השדה של אחד התושבים לשטח השדה של תושב אחר הוא 2:9

ביישומון הדינאמי במשימות 2-4, צריך לקבוע תחילה את מספר החלקות בכל אחד מהשדות. לאחר מכן, תוכלו לגרור את הנקודה הכחולה בקצה צלע המחיצות של כל אחד מהשדות ולקבל גרף נקודות המתאר את שטח כל אחד מהשדות השדה בהתאם לאורך צלע המחיצות שלה. תוכלו להיעזר בגרפים אלה כדי לקבוע את מידות השדות בדוגמה שלכם.

בכל דוגמה כתבו באפלט את מידות שני השדות שיצרתם. לאחר שכתבתם את מידות הצלעות תופיע בחלון הגרפי נקודה בצבע ירוק המתארת את שטח השדה הירוק  שיצרתם בהתאם לאורך צלע המחיצות שלו. כמו כן תופיע בחלון הגרפי נקודה בצבע כתום המתארת את שטח השדה הכתום שיצרתם בהתאם לאורך צלע המחיצות שלו. תוכלו להיעזר בנקודות אלה כדי לבדוק אם מידות השדה שהצעתם מתאימים לטענה.

משימה 5

במושב החליטו שאף תושב לא יחלק את השדה שלו ליותר מ-10 חלקות. כמו כן ועד המושב החליט שעל כל התושבים לגדר שדות באותו השטח. הם התלבטו איזה שטח לבחור עבור כל השדות במושב.

נתונות טענות.

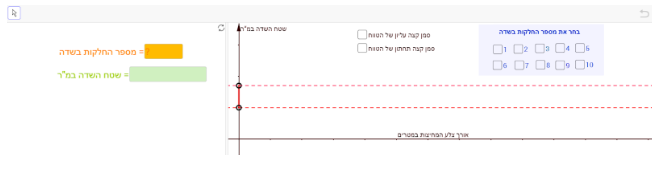
סמנו את הטענות הנכונות, ולכל טענה נכונה כתבו ביישומון הדינאמי את שטח השדה המתאים לטענה ובגרף סמנו את הטווח שעבורו הטענה נכונה.

הטענות:

1. אפשר לבחור שטח שדה שעבורו לא ניתן יהיה לחלק את השדות במושב ליותר מ 2 חלקות
2. אפשר לבחור שטח שדה שעבורו אפשר יהיה לחלק את השדות במושב לפחות ל-4 חלקות
3. אפשר לבחור כל שטח שרוצים ולגדר שדה ששטחו הוא כשטח שנבחר
4. אפשר לבחור שטח שדה שלא ניתן יהיה לגדר שדה עם השטח הנבחר שמחולק ל-2 חלקות.

הפעילות משלבת בין תכונות של פונקציה ריבועית לנושא שטח והיקף של מלבן, והיא כוללת פתרון של בעיית קיצון בעזרת תכונות של פונקציה ריבועית.

נושא תכונות של פונקציה ריבועית נלמד בכיתה ט' והוא כולל הסימטריות, קודוד הפרבולה, פתרון באמצעים אלגבריים וגרפיים, ותחומי ירידה ועלייה של הפונקציה הריבועית. (ראה עמוד  108   בתוכנית הלימודים של חט"ב)

 לכן, הפעילות מתאימה לתלמידי כיתה ט' עד י' אשר למדו את נושא הפונקציה הריבועית.

היקף ושטח של מלבן

כתיבת ביטוי אלגברי 

תכונות של פונקציה ריבועית

בתהליך כתיבה

בתהליך כתיבה 

• אחת המטרות של פעילות זו היא להראות את הקשר בין הגרף לבין מספר החלקות, כך שניתן לראות איך הגרף וגם נקודת המקסימום משתנים כשמספר החלקות משתנה.
• ניתן להראות לתלמידים שככל שמספר החלקות גדל, הערך של המקסימום קטן אבל הוא עדיין מתקבל עבור אותו ערך של אורך השדה (X).

• מטרה נוספת היא שימוש בתכונות הסימטריה בגרף של פונקציה ריבועית, ולהשתמש בציר סימטריה של הגרפים כדי להבין את היחסים בין שני הגרפים ולעשות השוואה ביניהם. 

• כדאי לדון עם התלמידים ולהראות שאורך צלע המחיצות הוא אותו אורך בכל השדות, לא משנה כמה חלוקות יש (120 = חצי מהאורך של הגדר).