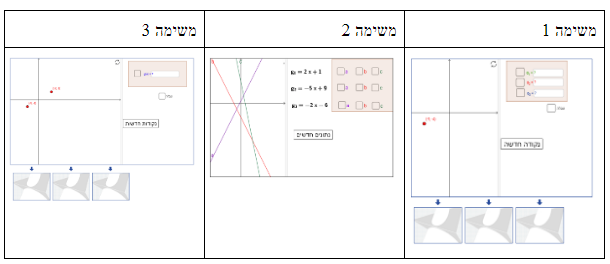
מתאימה לכיתות: ז',ח'.

מתאים לסלולר בתצוגה רוחבית
מטרת הפעילות היא לחזק את המיומנות האלגברית של פונקציה קווית.
הנושא של פונקציה קווית נלמד בדרך כלל בכיתות ח. הפעילות מתאימה כפעילות מסכמת בנושא של פונקציה קווית, פעילות חזרה בכיתה ט או פעילות בנושא של גיאומטריה אנליטית – קו ישר בתיכון ברמה של שלוש יחידות.
- שיפוע של פונקציה קווית
- משמעות נקודות על הצירים
- גרף שעובר בנקודות נתונות
- משמעות הפרמטרים בביטויים אלגבריים של פונקציה קווית f(x)=mx+b) ו- f(x)=m(x-p)
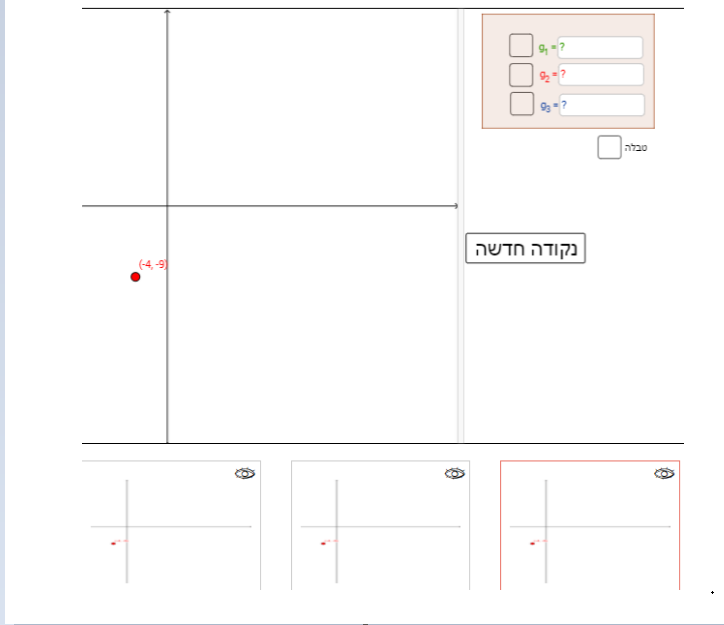
עבור משימה 1:
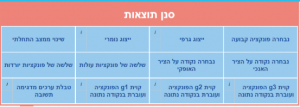
נבחרה פונקציה קבוע, ייצוג אלגברי, ייצוג נומרי, שינוי מצב התחלתי, נבחרה נקודה על הציר האנכי, נבחרה נקודה על הציר האופקי, שלשה של פונקציות עולות, שלשה של פונקציות יורדות, פונקציה קווית ועוברת בנקודה נתונה, טבלת ערכים מדגימה תשובה, שינוי ממצב התחלתי, נבחרה פונקציה קבוע.
נשים לב כי ישנו פילטר "נכונות" בפעילות זו מזהה מקרים בהם יצר התלמיד לפחות פונקציה אחת אשר מקיימת את תנאי הבעיה.
דוגמה לדיון על השטיח (במשימה מס' 1)
מה המאפיינים של השטיח? האם הפונקציות הם פונקציות עולות? יורדות? קבועות? איזה סוג של פונקציה לא קיימת בכלל במשימה? מדוע? (לא ניתן להקליד באפלט ייצוג אלגברי אשר מתאים לישרים המקבילים לציר ה – y) האם כל הפונקציות בשטיח אכן עוברות דרך הנקודה? האם ניתן להסתמך רק על "הראייה"? האם קיימת דרך לבדוק זאת? (שימוש בייצוג הנומרי)
עבור משימה 2:

– נבחרה פונקציה קבועה
– שלשה של פונקציות יורדות
– שלשה של פונקציות עולות
– נבחרה שלשה עם נקודת חיתוך משותפת
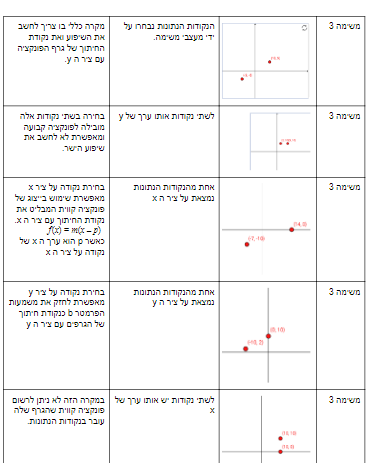
עבור משימה 3:

הפעילות עוסקת במיומניות אלגבריות, אך הגישה הפונקציונלית לאלגברה פותחת בפני תלמידים נקודות מבט נוספות למיומנוית אלה. בחירת נקודה על אחד הצירים מאפשרת שימוש בצורות שונות של ייצוג אלגברי של פונקציה קווית.
f(x)=mx+b מבליט את הפרמטר b כנקודת חיתוך של גרף הפונקציה עם ציר ה y
f(x)=m(x-p) מבליט את הפרמטר p כנקודת חיתוך של גרף הפונקציה עם ציר ה x
אפשר לדון על השונות בין התשובות. מדוע חלק בחרו בפונקציות עולות בלבד או יורדות בלבד? האם נבחרו נקודות מיוחדות? מה היו השיקולים לבחירת הנקודות. האם אכן בכל ההגשות כל שלושת הפונקציות שנבחרו עברו דרך הנקודה?האם נעשה שימוש בייצוג נומרי? במה ייצוגים שונים עוזרים במשימה?