הקדמה לכל המשימות: 

לפניכם אפליקציה לסרטוט משולשים.

בחלון השמאלי של היישומון נתונה נקודה צהובה במערכת הצירים, אותה תוכלו למקם במקומות שונים במערכת הצירים וליצור משולש מתאים לדרישות לגבי זוויותיו.

בחלון הימני תוכלו לשנות את אורכה של צלע המשולש עליה מונחות הזוויות x ו-y.

תוכלו לשפר את האפליקציה ולמיין בעזרתה סוגי משולשים על ידי יצירת קטעים או תחומים שבהם תנוע הנקודה הצהובה במערכת הצירים. 

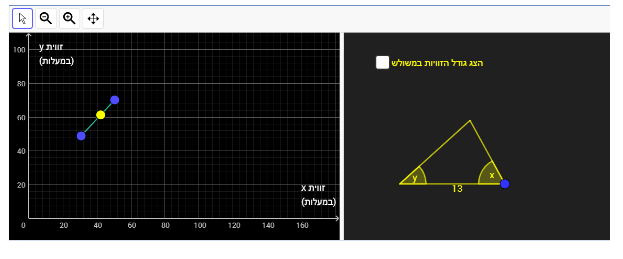
במשימה 1 נתונה טענה: בחלון השמאלי ביישומון קיים קטע (לא חובה שיכלול את קצותיו) כך שכל נקודה עליו יוצרת בחלון הימני משולש ישר זווית.  

התלמיד מתבקש לגרור את הנקודות הכחולות בחלון השמאלי ולהגיש 3 קטעים שונים כאלה.

ניתן לראות את המשולשים המתקבלים על ידי גרירת הנקודה הצהובה על הקטע שיצר התלמיד.

המטרה של משימה זו היא לדון עם התלמידים על סכום זוויות במשולש. כמו כן, לחשוב על הקשר בין הזוויות x ו- y במקרה שזווית z היא זווית ישרה, ועל סמך זה לעורר דיון על פונקציות ועל סוגי ישרים (פונקציה קווית יורדת, פונקציה קבועה = ישר מקביל לציר X, ישר מקביל לציר Y).  

במשימה 2 נתונות טענות.

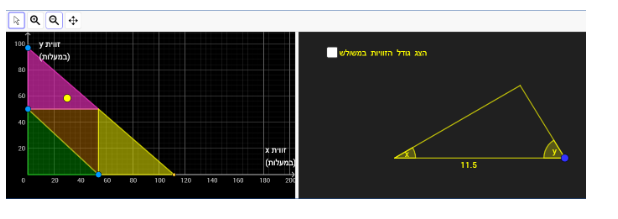
1. בחלון השמאלי ביישומון, קיים משולש צהוב כך שכל נקודה בתוכו תיצור בחלון הימני משולש קהה זווית.
2. בחלון השמאלי ביישומון, קיים משולש סגול כך שכל נקודה בתוכו תיצור בחלון הימני משולש קהה זווית.
3. בחלון השמאלי ביישומון, קיים משולש חום כך שכל נקודה בתוכו תיצור בחלון הימני משולש חד זוויות.
4. בחלון השמאלי ביישומון, קיים משולש ירוק כך שכל נקודה בתוכו תיצור בחלון הימני משולש קהה זווית.

התלמיד מתבקש להגיש לכל טענה דוגמה תומכת על ידי גרירת הנקודות הכחולות בחלון השמאלי.

ניתן לראות את המשולשים המתקבלים על ידי גרירת הנקודה הצהובה במשולשים הצבעוניים שיצרתם.

המטרה של משימה זו היא למצוא את התחום שבו כל המשולשים עונים על הדרישה של הטענה, לדון במקרים השונים והאם התחום מכיל את כל המשולשים האפשריים. 

במשימה 3 נתונות טענות.  

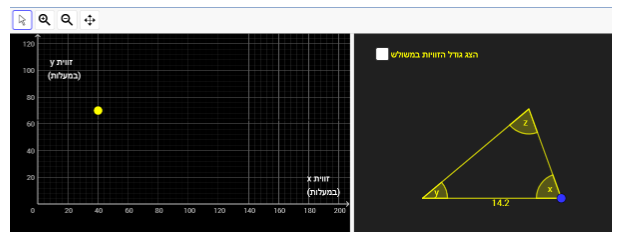
1. קיימת נקודה צהובה בחלון השמאלי היוצרת משולש שווה שוקיים שזווית הראש שלו היא זווית z
2. קיימת נקודה צהובה בחלון השמאלי היוצרת משולש שווה שוקיים שזווית הראש שלו היא זווית x
3. קיימת נקודה צהובה בחלון השמאלי היוצרת משולש שווה שוקיים שזווית הראש שלו היא זווית y.

התלמיד מתבקש להגיש לכל טענה דוגמה תומכת על ידי גרירת הנקודה הצהובה בחלון השמאלי למקום מתאים.

המטרה של משימה זו היא לבדוק אם התלמיד מכיר את התכונות של משולש שווה שוקיים, ולדון בקשר בין הזוויות במשולש כזה.  

מטרה נוספת היא לעורר דיון לגבי מיקום כל הנקודות במערכת הצירים המקיימות שוויון בין שתי זוויות במשולש.   

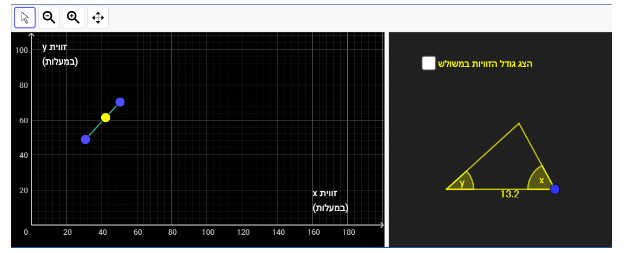
במשימה 4  נתונה טענה: בחלון השמאלי ביישומון קיים קטע (לא חובה שיכלול את קצות הקטע) כך שכל נקודה עליו יוצרת בחלון הימני משולש שווה שוקיים.

התלמיד מתבקש לגרור את הנקודות הכחולות בחלון השמאלי ולהגיש 3 קטעים שונים כאלה.

ניתן לראות את המשולשים המתקבלים על ידי גרירת הנקודה הצהובה על הקטע שיצר התלמיד.

המטרה של משימה זו היא לדון במיקום של כל הנקודות במערכת הצירים המקיימות שוויון בין שתי זוויות במשולש, ולדבר על שלושת המקרים: זווית x היא הראש, זווית y היא הראש, זווית z היא הראש. 

במשימה 5 נתונה טענה: בחלון השמאלי בישומון קיים קטע (ללא קצות הקטע) שכולו באחד התחומים, כך שכל נקודה עליו יוצרת בחלון הימני משולש שווה שוקיים חד זוויות.

התלמיד מתבקש לגרור את הנקודות הכחולות בחלון השמאלי למקום מתאים ולגרור את הנקודות הכחולות בקצות הקטע למקום מתאים ולהגיש 3 קטעים שונים שתומכים בטענה.

ניתן לראות את המשולשים המתקבלים על ידי גרירת הנקודה הצהובה על הקטע שיצר התלמיד.

המטרה של משימה זו היא למצוא את התחום שבו כל המשולשים עונים על הדרישה של הטענה (משולש שווה שוקיים וגם חד זוויות) והאם התחום מכיל את כל המשולשים האפשריים.

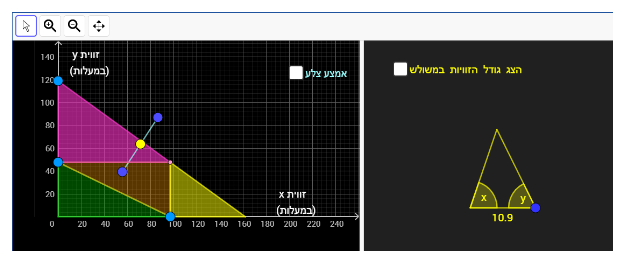
במשימה 6 נתונה טענה: בחלון השמאלי בישומון קיים קטע (ללא קצות הקטע) שכולו באחד התחומים, כך שכל נקודה עליו יוצרת בחלון הימני משולש שווה שוקיים קהה זווית.

התלמיד מתבקש לגרור את הנקודות הכחולות בחלון השמאלי למקום מתאים ולגרור את הנקודות הכחולות בקצות הקטע למקום מתאים ולהגיש 3 קטעים שונים שתומכים בטענה.

ניתן לראות את המשולשים המתקבלים על ידי גרירת הנקודה הצהובה על הקטע שיצר התלמיד.

המטרה של משימה זו היא למצוא את התחום שבו כל המשולשים עונים על הדרישה של הטענה (משולש שווה שוקיים וגם קהה זווית) והאם התחום מכיל את כל המשולשים האפשריים.

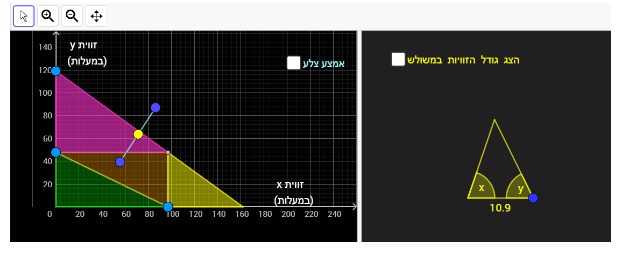
פעילות זו עוסקת בכמה נושאים: סוגי משולשים, מערכת צירים, וכתיבת ביטויים אלגבריים המתארים קשר בין זוויות המשולש. נושאים אלה נלמדים בכיתה ז'.

בפעילות זו ניתן להתייחס גם לנושא גרף של פונקציה קווית המתארת את הקשר בין זוויות המשולש (בפרט הפונקציות  y=x , y=180-2x , x=180-2y, y=90-x  ) .

 (ראה עמוד  40   בתוכנית הלימודים של חט"ב)

לכן פעילות זו מתאימה לתלמידים בכיתות ז'-ח' כפעילות תרגול וחזרה. 

סוגי המשולשים

חישובי זוויות במשולש

הכרת מערכת צירים

כתיבת ביטויים אלגבריים המתארים קשר בין זוויות

משימה 1 

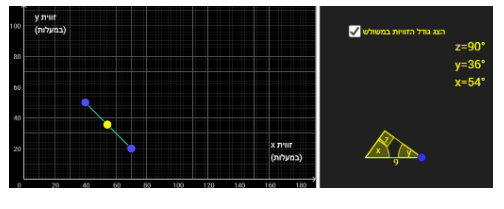
ישנם 3 מקרים שונים המקיימים את הטענה:

1) כאשר זווית y היא הישרה = קטע אופקי המקביל לציר x כך ש- y=90 (חלק מישר שהוא פונקציה קבועה) 

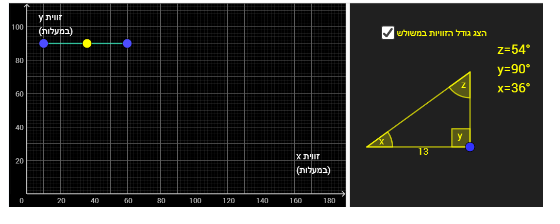
2) כאשר זווית x היא הישרה =קטע אנכי המקביל לציר y כך ש- x=90 (חלק מישר שאינו פונקציה)

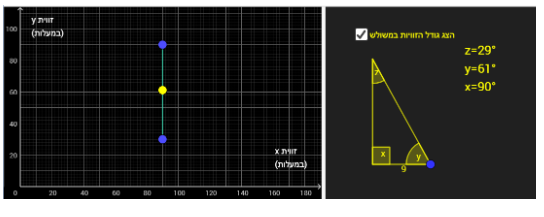
3)  כאשר זווית z היא הישרה = קטע שכל נקודה עליו מקיימת x+y=90 (חלק מפונקציה קווית y=90-x ) 

משימה 2 

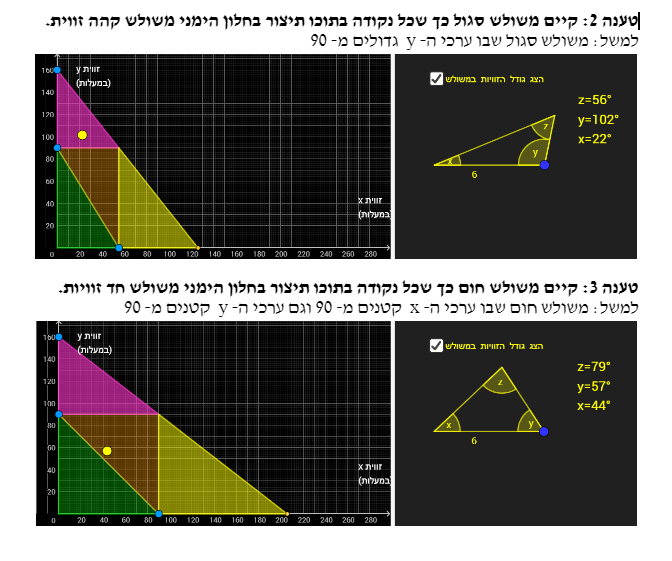
טענה 1: קיים משולש צהוב כך שכל נקודה בתוכו תיצור בחלון הימני משולש קהה זווית.

למשל: משולש צהוב שבו ערכי ה- x  גדולים מ- 90

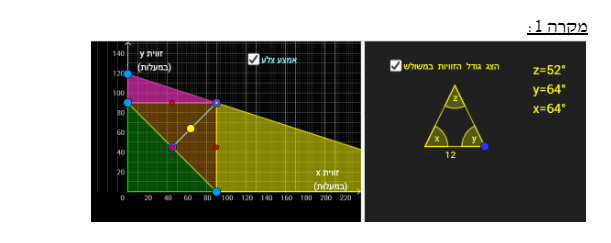
משימה 3

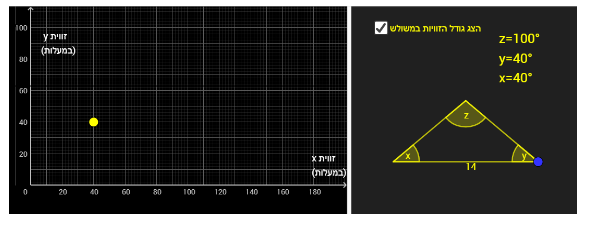
טענה 1: קיימת נקודה בחלון הימני היוצרת משולש שווה שוקיים שזווית הראש שלו היא זווית z .

זה מתקיים כאשר ערכי ה- x וה- y של הנקודה שווים ( x=y ).

למשל:

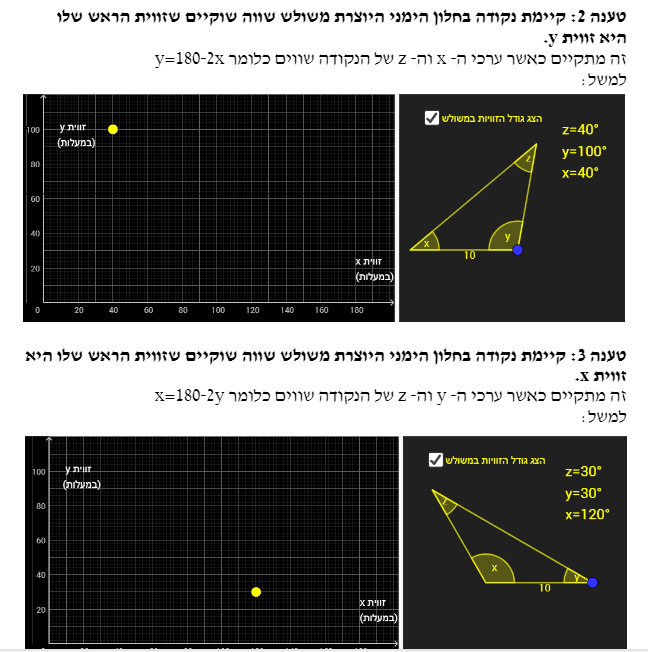
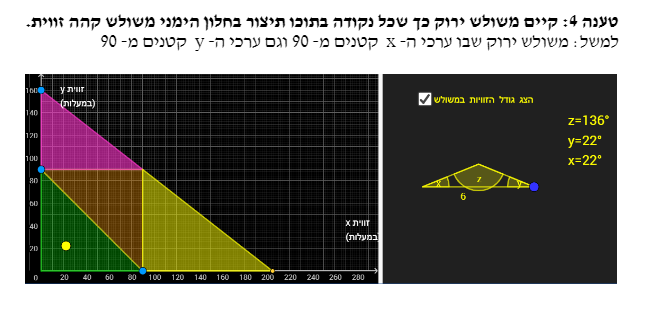
משימה 4 

ישנם 3 מקרים שונים המקיימים את הטענה:

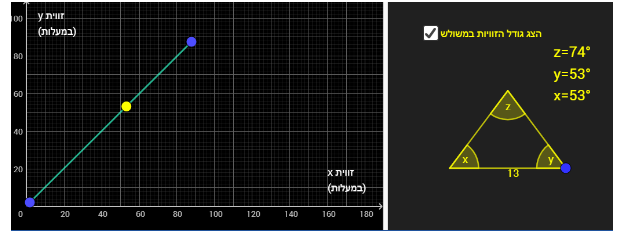
1) כאשר זווית z היא זווית הראש = קטע שכל נקודה עליו מקיימת שערכי ה- x וה- y שלה שווים (חלק מישר שהוא פונקציה עולה y=x ) 

משימה 5 

כדי שטענה זו תתקיים, צריך קודם כל למצוא את התחום שבו כל המשולשים הם חדי זוויות (מצאנו במשימה 2 טענה 3), לאחר מכן למקם את הקטע על חלק מהישר שעליו נמצאות כל הנקודות היוצרות משולשים שווה שוקיים.

ניתן להיעזר בכלי "אמצע צלע".

ישנם 3 ישרים שונים כך שכל נקודה עליהם יוצרת משולש שווה שוקיים (מצאנו במשימה הקודמת) ולכן ישנם 3 מקרים המקיימים את הטענה:

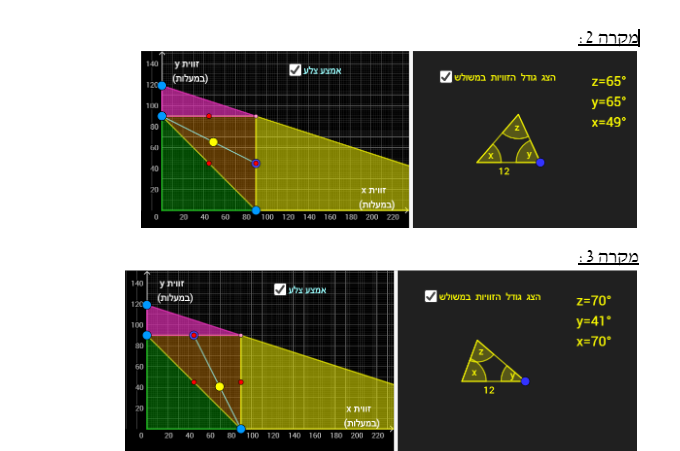
משימה 6

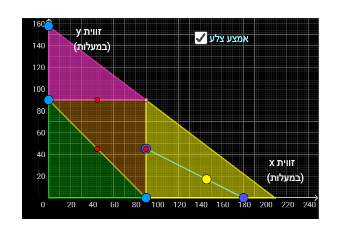
כדי שטענה זו תתקיים, צריך קודם כל למצוא את התחום שבו כל המשולשים הם קהה זווית, לאחר מכן למקם את הקטע על חלק מהישר שעליו נמצאות כל הנקודות היוצרות משולשים שווה שוקיים.

ניתן להיעזר בכלי "אמצע צלע".

ישנם 3 תחומים שונים כך שכל נקודה בהם יוצרת משולש קהה זווית (מצאנו במשימה 2), כמו כן ישנם 3 ישרים שונים כך שכל נקודה עליהם יוצרת משולש שווה שוקיים (מצאנו במשימה 4). 

מכאן, מקבלים 3 מקרים המקיימים את הטענה:

מקרה 1:

משולש צהוב כך שכל נקודה בתוכו תיצור בחלון הימני משולש קהה זווית (שבו ערכי ה- x  גדולים מ- 90) וגם קטע שכל נקודה עליו מקיימת שערכי ה- z וה- y שלה שווים

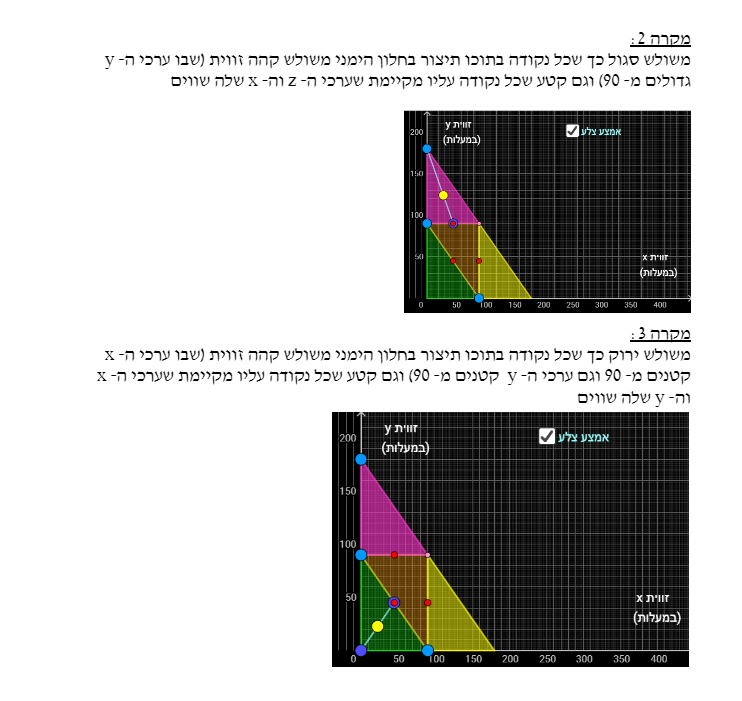
בתהליך כתיבה

• יש לוודא שתלמידים מבינים את המעבר מייצוג נקודה על מערכת הצירים לייצוג המשולש.

משימה 1

יש לדון במקרים השונים התומכים בטענה הנתונה:

• מקרה 1 שבו זווית y היא הישרה. במקרה זה הקטע צריך להיות מקביל לציר x. 

ניתן להתייחס לביטוי האלגברי המתאר את הישר y=90 שכולל את כל הקטעים המקיימים את הטענה, ובמידת האפשר להתייחס לכך שהישר הוא גרף של פונקציה קבועה. 

• מקרה 2 שבו זווית x היא הישרה. במקרה זה הקטע צריך להיות מקביל לציר y. ניתן להתייחס לביטוי האלגברי המתאר את הישר x=90  שכולל את כל הקטעים המקיימים את הטענה, ובמידת האפשר להתייחס לכך שהישר לא מתאר פונקציה.
• מקרה 3 שבו זווית z היא הישרה. במקרה זה הקטע צריך להיות על הישר x+y=90.  במידה והתלמידים לא מגישים דוגמאות שבהן זווית z היא הישרה, יש לדון במקרה זה ובמידת האפשר לדבר על הפונקציה הקווית y=90-x  

משימה 2

• בכל אחת מהטענות 1,2,4 – מי מהזוויות של המשולש היא הזווית הקהה? 
• האם כל המשולשים בתוך המשולש הצבעוני שיצרתם תומכים בטענה? 
• למה המשולש הצבעוני שיצרתם תמיד תומך בטענה?  
• האם קיים משולש צבעוני גדול יותר מהמשולש שיצרתם שגם תומך בטענה?
• מה הוא ערך ה- x המינימלי/המקסימלי ומה הוא ערך ה- y המינימלי/המקסימלי בכל אחד מהמשולשים הצבעוניים שיצרתם?

משימה 3

• בטענה 1 – מה הוא הקשר בין הזוויות x ו- y ?
• בטענה 2 – מה צריכים להיות ערכי y כדי ש- z=x ? 
• בטענה 3 – מה צריכים להיות ערכי x כדי ש- y=z ?  

משימה 4

• יש לדון בכל המקרים המקיימים את הטענה (המקרים שהופיעו במשימה הקודמת), בנוסף, יש לדון על הקשר בין זוויות המשולש ולנסח ביטויים אלגבריים מתאימים המתארים פונקציות:

1. כאשר זווית z היא זווית הראש = קטע שכל נקודה עליו מקיימת שערכי ה- x וה- y שלה שווים (חלק מישר שהוא פונקציה עולה y=x ) 
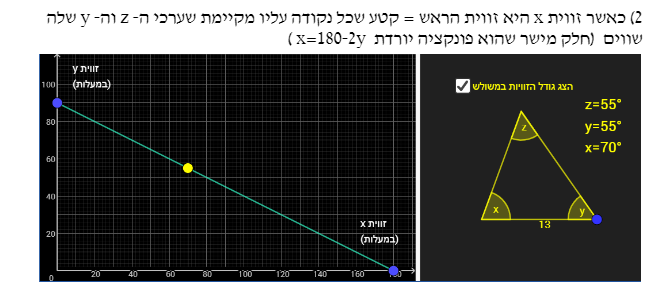
2. כאשר זווית x היא זווית הראש = קטע שכל נקודה עליו מקיימת שערכי ה- z וה- y שלה שווים  (חלק מישר שהוא פונקציה יורדת  x=180-2y ) 
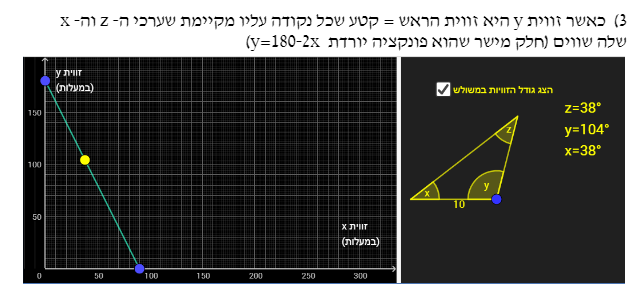
3. כאשר זווית y היא זווית הראש = קטע שכל נקודה עליו מקיימת שערכי ה- z וה- x שלה שווים (חלק מישר שהוא פונקציה יורדת  y=180-2x) 

• אפשר לדון בתכונות הפונקציות השונות (שיפוע שונה, פונקציה עולה/יורדת): 

y=x , x=180-2y , y=180-2x 

משימה 5

• יש לוודא שהתלמידים מבינים את תהליך הפתרון: צריך קודם כל למצוא את התחום שבו כל המשולשים הם חדי זוויות – שזה המשולש החום שבו ערכי ה- x קטנים מ- 90 וגם ערכי ה- y קטנים מ- 90  (מצאנו במשימה 2 טענה 3), לאחר מכן למקם את הקטע על חלק מהישר שעליו נמצאות כל הנקודות היוצרות משולשים שווה שוקיים- שזה הישר y=x  או הישר y=180-2x או הישר x=180-2y (מצאנו במשימה 4).

• יש לדון ב- 3 מקרים המקיימים את הטענה:

1. הקטע כולו במשולש החום וגם נמצא על הישר y=x
2. הקטע כולו במשולש החום וגם נמצא על הישר y=180-2x
3. הקטע כולו במשולש החום וגם נמצא על הישר x=180-2y כלומר y=90-x/2 

• במידה ולא נכתבו ביטויים אלגבריים המתארים את 3 המקרים, יש להתייחס לזה במשימה זו. 

משימה 6 

• יש לוודא שהתלמידים מבינים את תהליך הפתרון: צריך קודם כל למצוא את כל התחומים שבהם כל המשולשים הם קהה זווית (מצאנו במשימה 2), לאחר מכן למקם את הקטע על חלק מהישר שעליו נמצאות כל הנקודות היוצרות משולשים שווה שוקיים – שזה הישר y=x  או הישר y=180-2x או הישר x=180-2y (מצאנו במשימה 4).
• יש לדון ב- 3 מקרים המקיימים את הטענה:

1. הקטע כולו במשולש הצהוב שבו ערכי ה- x  גדולים מ- 90, וגם נמצא על הישר x=180-2y כלומר y=90-x/2 .
2. הקטע כולו במשולש הסגול שבו ערכי ה- y  גדולים מ- 90, וגם נמצא על הישר y=180-2x. 
3. הקטע כולו במשולש הירוק שבו ערכי ה- x  קטנים מ- 90 וגם ערכי ה- y  קטנים מ- 90, וגם נמצא על הישר y=x. 

• איך נקודות האמצע עוזרות בפתרון?