פעילות זו עוסקת בזיהוי משולשים שווה שוקיים וישרי זווית, ושימוש בתכונות של משולש שווה שוקיים (זוויות בסיס שוות, הגובה לבסיס מתלכד עם התיכון). כמו כן הבנת הקשר בין הסיפור/התיאור המילולי לשרטוט המתאר את המפה האינטראקטיבית.

מטרה נוספת של הפעילות היא להגיע בדיון הכיתתי לנימוקים והוכחות בגאומטריה תוך התייחסות לדוגמאות שהתלמיד הגיש. לפעמים הדוגמה מאפשרת לראות את הנימוק מידית ולפעמים מורכב יותר לראות את הנימוק.

רקע למשימות:

בחפירה ארכיאולוגית של עיר מבצר עתיקה נמצאה מגילה ישנה ובה צוינו מקומות שונים בעיר  ומיקומו של מאגר המים התת קרקעי נקבע בהתאם למקומות שצוינו.

במגילה נכתב:

"את מאגר המים התת קרקעי חפרנו במקום מוסתר כך שאויבים לא יזהמו את המים במאגר:

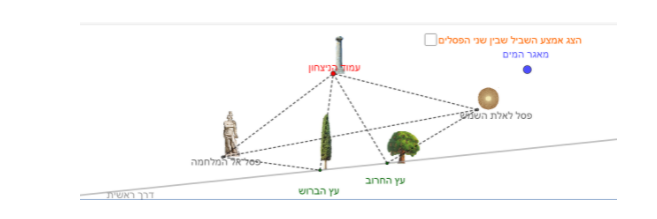
צעדנו בקו ישר לאורך השביל מעמוד הניצחון עד לעץ החרוב העתיק שעמד לצד הדרך הראשית. ליד עץ החרוב פנינו שמאלה 90 מעלות וצעדנו ישר את אותו המרחק שצעדנו בין העמוד לעץ החרוב. במקום אליו הגענו בנינו פסל לאלת השמש. לאחר מכן חזרנו לעמוד הניצחון וצעדנו בקו ישר לאורך השביל עד לעץ הברוש הגבוה שאף הוא עמד לצד הדרך הראשית. ליד עץ הברוש פנינו 90 מעלות ימינה וצעדנו בקו ישר את אותו המרחק שבין עמוד הניצחון לעץ הברוש. במקום אליו הגענו הקמנו פסל לאל המלחמה.

את הפתח למאגר המים חפרנו באמצע השביל שבין שני הפסלים. "

 הארכיאולוגים שהגיעו לאי גילו שכל השבילים נעלמו, כך גם עמוד הניצחון והפסלים. ורק הדרך הראשית, עץ הברוש הגבוה ועץ החרוב העתיק עמדו במקומם. לפיכך הם התקשו גם לאתר את הפתח למאגר המים.

החוקרים החליטו לבנות מפה ממוחשבת אינטראקטיבית שתאפשר להם לחקור מקומות שונים בהם יכלו לעמוד עמוד הניצחון, שני הפסלים המוזכרים במגילה והפתח למאגר המים התת קרקעי.  

שימו לב, במשימות 1-3 מתייחסות למסקנות הנובעות מהשערות של חוקרים על סמך חפירות באתרים אחרים ומה ניתן להסיק על סמך השערות אלה. אך אין ודאות שהשערותיהם אכן נכונות. משימה 4 מתייחסת לעובדות בשטח ללא הסתמכות על השערות כלשהם מאתרים אחרים. 

משימה 1: 

במשימה הראשונה נתון שאחד החוקרים משער כי השביל בין עמוד הניצחון לפסל אלת השמש צריך להיות מאונך לשביל שבין עמוד הניצחון לפסל אל המלחמה. התלמיד מתבקש להגיש 3 דוגמאות שונות למיקום עמוד הניצחון שמתאים להשערה זו.

המטרה של משימה זו היא שתלמיד יוכיח שעמוד הניצחון  חייב להיות בהתאם להשערה זו על הדרך הראשית. (ראו דיון והוכחה ב"דוגמאות להגשה")

משימה 2:

במשימה השנייה נתון שחוקר אחר משער כי השביל המחבר בין עמוד הניצחון לעץ החרוב צריך להיות מאונך לשביל בין העמוד הניצחון לעץ הברוש. התלמיד מתבקש להגיש 3 דוגמאות שונות למיקום אפשרי של עמוד הניצחון שמתאים להשערה זו.

המטרה של משימה זו היא לדון מדוע  עמוד הניצחון חייב  להיות על השביל שבין הפסלים או על ההמשך שלו.

(ראו דיון והוכחה ב"דוגמאות להגשה")

משימה 3:

במשימה השלישית נתון שחוקר שלישי משער כי עמוד הניצחון צריך להיות במרחק שווה משני העצים. התלמיד מתבקש להגיש 3 דוגמאות שונות למיקום אפשרי של עמוד הניצחון שמתאים להשערה זו.

המטרה של משימה זו היא לדון מדוע עמוד הניצחון חייב להיות על האנך האמצעי לקטע הדרך שבין שני העצים.

שימו לב, במשימה זו ניתן להיעזר בכלי "אנך" בסרגל הכלים.

(ראו דיון והוכחה ב"דוגמאות להגשה")

משימה 4:

בשונה מהמשימות הקודמות, משימה 4 מתייחסת לטענות שתמיד מתקיימות ולא השערות שמתקיימות במקרים פרטיים.

במשימה זו נתונות 4 טענות. התלמיד מתבקש לבחור את הטענות הלא נכונות ולכל טענה להגיש דוגמה המפריכה אותה.

משימה 5:

במשימה החמישית נתון כי הארכיאולוגים שהגיעו לאי גילו שכל השבילים נעלמו, כך גם עמוד הניצחון, הפסלים, והפתח למאגר המים. ורק הדרך הראשית עץ הברוש הגבוה ועץ החרוב העתיק עמדו במקומם.

אחרי שחקרו את המפה הדינמית, הארכיאולוגים החליטו שאין בעיה למצוא את הפתח למאגר המים למרות שמה שנותר מהתיאור במגילה הוא עץ הברוש ועץ החרוב בלבד.

התלמיד נדרש לשרטט מפה שבעזרתה ניתן למצוא את הפתח למאגר המים.

המטרה של משימה זו היא ליישם את המסקנות שהתקבלו ממשימה 4 לגבי הטענות שתמיד מתקיימות.  

לפי תוכנית הלימודים של חט"ב, בלימודי הגאומטריה בכיתה ט' התלמידים לומדים לראשונה להוכיח משפטים במסגרת היסקית המושתתת על הנחות יסוד והגדרות. במסגרת זו הם לומדים גם להתנסח באופן פורמאלי כך שהם נדרשים לתכנן הוכחה ולנסחה.

יש להקפיד שכל טענה משמעותית במהלך הוכחה תהיה מלווה בנימוק.

(ראה עמוד  116   בתוכנית הלימודים של חט"ב)

 פעילות זו עוסקת בהבנת אובייקטים גיאומטריים וחקירתם בעזרת יישומון אינטראקטיבי. 

המטרה הכללית של הפעילות היא להגיע בדיון הכיתתי לנימוקים והוכחות בגאומטריה תוך התייחסות לדוגמאות שהתלמיד הגיש. לפעמים הדוגמה מאפשרת לראות את הנימוק מידית ולפעמים מורכב יותר לראות את הנימוק.

הפעילות מתאימה להעברה בסוף כיתה ח' או בכיתה ט' כהקדמה לנושא הוכחות פורמליות של משפטים בגאומטריה. 

• הבנת הקשר בין הסיפור/התיאור המילולי לשרטוט המתאר את המפה האינטראקטיבית.
• זיהוי משולשים שווה שוקיים ומשולשים ישרי זווית בשרטוט.
• שימוש בתכונות של משולש שווה שוקיים (זוויות בסיס שוות, הגובה לבסיס מתלכד עם התיכון)

סכום זוויות במשולש

 תכונות ותנאים של משולש שווה שוקיים

תכונות משולש ישר זווית ושווה שוקיים

זווית שטוחה

משימה 1: 

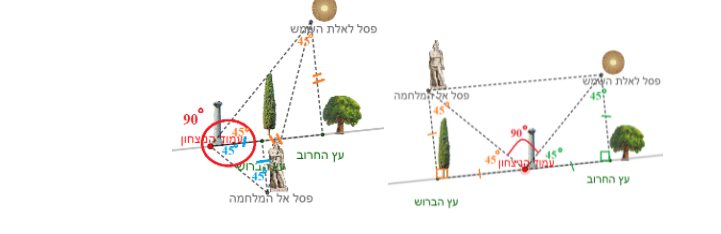
כדי שהשביל בין עמוד הניצחון לפסל אלת השמש יהיה מאונך לשביל שבין עמוד הניצחון לפסל אל המלחמה, המיקום של עמוד הניצחון צריך להיות על הדרך הראשית (על הקטע בין שני העצים או לאורך הדרך מחוץ לקטע שבין העצים).

דוגמאות:

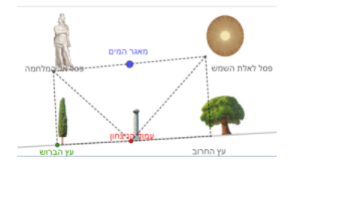
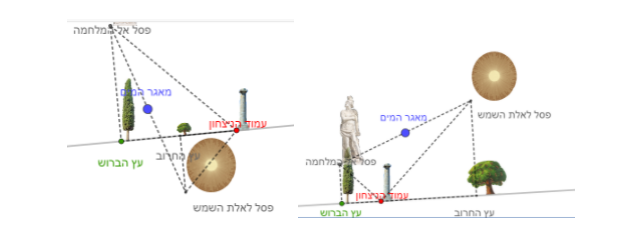
בשני המקרים, אפשר להוכיח את זה באמצעות שימוש בסכום זוויות במשולש שווה שוקיים וישר זווית:

משימה 2: 

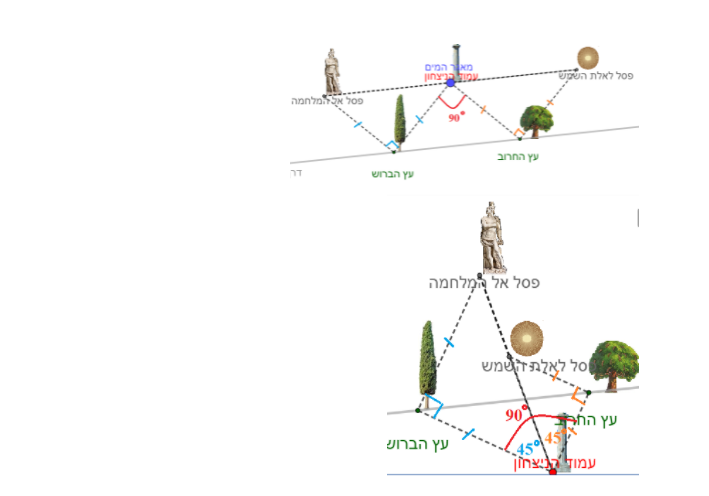
אפשרות 1 – עמוד הניצחון נמצא על השביל שבין שני הפסלים.

אפשרות 2 (מקרה פרטי של אפשרות 1) – עמוד הניצחון נמצא באמצע השביל שבין שני הפסלים, כלומר באותו מיקום של מאגר המים.

אפשרות 3 – עמוד הניצחון נמצא על המשך השביל שבין שני הפסלים.

בכל המקרים, אפשר להוכיח את זה באמצעות שימוש בסכום זוויות במשולש שווה שוקיים וישר זווית:

משימה 3: 

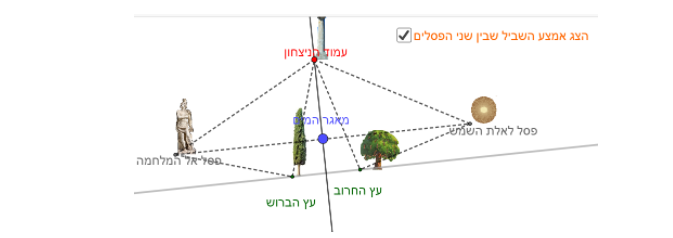
כדי שהמרחק של עמוד הניצחון משני העצים יהיה שווה, מיקום עמוד הניצחון צריך להיות על האנך האמצעי לקטע הדרך שבין שני העצים. 

כדי להוכיח את זה,  התלמיד אמור להוריד אנך מעמוד הניצחון לדרך הראשית כך שיעבור באמצע השביל שבין שני הפסלים (מיקום מאגר המים), וזה בהסתמך על המשפט: אם הגובה והתיכון מתלכדים במשולש אז המשולש הוא שווה שוקיים.

משימה 4: 

טענה 1 ו- 3 תמיד נכונות. (ראו הוכחה ב"דיון")

טענה 2 לא תמיד נכונה, היא מתקיימת רק כאשר עמוד הניצחון נמצא על הישר המקביל לדרך הראשית. כל מיקום אחר של עמוד הניצחון מפריך את הטענה. 

 משימה 5:

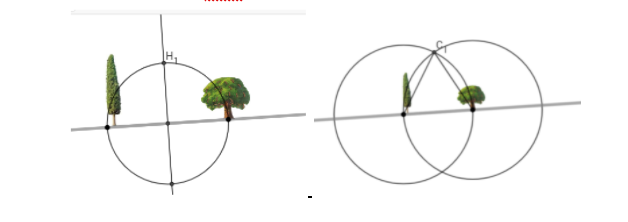
בהסתמך על המסקנות ממשימה 4, מקבלים שמאגר המים תמיד נמצא במרחק שווה משני העצים. 

דוגמאות לשרטוטי מפה שבעזרתה ניתן למצוא את הפתח למאגר המים:

משימה 1:

דרישות:

השביל בין עמוד הניצחון לפסל אלת השמש מאונך לשביל שבין עמוד הניצחון לפסל אל המלחמה

מאפיין נכונות:

עמוד הניצחון נמצא לאורך הדרך הראשית

מאפייני עבודה:

עמוד הניצחון הוא על הקטע בין שני העצים

עמוד הניצחון בדיוק באמצע הקטע בין שני העצים 

הוצג אמצע השביל שבין שני הפסלים

סומן מקום מתאים למאגר המים 

משימה 2:

דרישות:

השביל בין עמוד הניצחון לעץ החרוב מאונך לשביל בין עמוד הניצחון לעץ הברוש

מאפיין נכונות:

עמוד הניצחון נמצא על השביל שבין שני הפסלים

מאפייני עבודה:

עמוד הניצחון נמצא באותו מיקום של מאגר המים

עמוד הניצחון נמצא על המשך השביל שבין שני הפסלים

הוצג אמצע השביל שבין שני הפסלים

סומן מקום מתאים למאגר המים 

משימה 3: 

דרישות: 

המרחק של עמוד הניצחון משני העצים יהיה שווה

מאפייני נכונות: 

עמוד הניצחון נמצא על האנך האמצעי לקטע הדרך שבין שני העצים

מאפייני עבודה: 

השתמשו באנך מעמוד הניצחון לדרך הראשית 

האנך האמצעי עובר באמצע השביל שבין שני הפסלים

סומן מקום מתאים למאגר המים 

משימה 4: 

נבחרה טענה 1 

נבחרה טענה 2

נבחרה טענה 3 

מאפייני עבודה לטענה 2: 

עמוד הניצחון נמצא על הישר המקביל לדרך הראשית

עמוד הניצחון נמצא באותו מיקום של מאגר המים

משימה 1:

• בכיתה אפשר לבקש מהתלמידים לנסח את הטענה שלהם לפי הדוגמאות שהציעו. ולנסות לנסח טענה כללית יותר שתתאים לכלל הדוגמאות האפשריות.
• הטענה הכללית במקרה הזה היא  "אם השביל בין עמוד הניצחון לפסל אלת השמש מאונך לשביל שבין עמוד הניצחון לפסל אל המלחמה אז עמוד הניצחון נמצא על הדרך הראשית."
• טענות פחות כלליות שיכולות לעלות:

"אם השביל בין עמוד הניצחון לפסל אלת השמש מאונך לשביל שבין עמוד הניצחון לפסל אל המלחמה אז עמוד הניצחון נמצא על הדרך הראשית בין שני העצים."

• אפשר לדון בכיתה גם במשפט ההפוך שיתכן שתלמידים ינסחו:

 "אם עמוד הניצחון נמצא על הדרך הראשית אז השביל בין עמוד הניצחון לפסל אלת השמש מאונך לשביל שבין עמוד הניצחון לפסל אל המלחמה." אפשר לדון האם במקרה הזה  גם המשפט הישר וגם ההפוך נכונים ומדוע.

• גם בנימוקים אפשר לדון בכאלה שמצדיקים את נכונות הטענה עבור דוגמה פרטית לכאלה המצדיקים את נכונות הטענה הכללית. אפשר גם לדון בהוכחה בדרך השלילה.

משימה 2:

• גם במשימה זו יש לבקש מהתלמידים לנסח את הטענה שלהם לפי הדוגמאות שהציעו. ולנסות לנסח טענה כללית יותר שתתאים לכלל הדוגמאות האפשריות.
• הטענה הכללית במקרה הזה היא  "אם השביל בין עמוד הניצחון עץ החרוב מאונך לשביל שבין עמוד הניצחון לעץ הברוש אז עמוד הניצחון נמצא על הדרך השביל בין פסל אל המלחמה לפסל אלת השמש או על המשכו של השביל הזה."
• טענות פחות כלליות שיכולות לעלות:

"אם השביל בין עמוד הניצחון לעץ הברוש מאונך לשביל בין עמוד הניצחון לעץ החרוב אז עמוד הניצחון נמצא על השביל  בין שני הפסלים (אלת השמש, ואל המלחמה)."

• אפשר לדון בכיתה גם במשפט ההפוך שיתכן שתלמידים ינסחו:

"אם עמוד הניצחון נמצא על השביל בין שני הפסלים (אלת השמש, ואל המלחמה) או על המשכו של שביל זה אז השביל בין עמוד הניצחון לעץ החרוב מאונך  לשביל שבין עמוד הניצחון לעץ הברוש". אפשר לדון האם במקרה הזה  גם המשפט הישר וגם ההפוך נכונים ומדוע.

• בנימוקים אפשר לדון בכאלה שמצדיקים את נכונות הטענה עבור דוגמה פרטית ובכאלה המצדיקים את נכונות הטענה הכללית. גם במקרה זה אפשר גם לדון בהוכחה בדרך השלילה.
• כדאי לדון בכיתה גם במקרה הקצה בו פסל אלת השמש ופסל אל המלחמה הוצבו באותו המקום.

 משימה 3:

• גם במשימה זו לבקש מהתלמידים לנסח את הטענה שלהם לפי הדוגמאות שהציעו. ולנסות לנסח טענה כללית יותר שתתאים לכלל הדוגמאות האפשריות.
• גם כאן אפשר לדון בכיתה במשפט ההפוך שיתכן שתלמידים ינסחו. בנימוקים אפשר לדון בכאלה שמצדיקים את נכונות הטענה עבור דוגמה פרטית ובכאלה המצדיקים את נכונות הטענה הכללית. גם במקרה זה אפשר גם לדון בהוכחה בדרך השלילה.
• גם במקרה הזה כדאי לדון בדוגמאות קצה: עמוד הניצחון נמצא בפתח מאגר המים או עמוד הניצחון  נמצא באמצע המרחק שבין שני העצים.
• יש לשים לב כי משימה זו עוסקת בגובה לבסיס ותיכון במשולש שווה שוקיים, אך אין שימוש ב"חוצה זווית הראש".
• נקודה לדיון בכיתות הגבוהות " מה הוא המקום הגיאומטרי של מיקום עמוד הניצחון המתאים להשערה הנתונה?"

משימה 4:

• יש לציין בכיתה שהטענות הללו מתייחסות לתיאור המקומות במשימה בלי קשר להשערות שהעלו החוקרים.
• יש לדון עם התלמידים האם המקום של מאגר המים תלוי במיקום של עמוד הניצחון?

• הוכחה כללית שהמיקום של מאגר המים לא משתנה ואינו תלוי במיקום של עמוד הניצחון:

נסמן:

עמוד הניצחון = A

אל השמש = E

אל המלחמה = C

עץ הברוש = B

עץ החרוב = D

נתון ש- F (מאגר המים) אמצע CE

צריך להוכיח ש F נמצא תמיד על האנך האמצעי של המשולש BDF

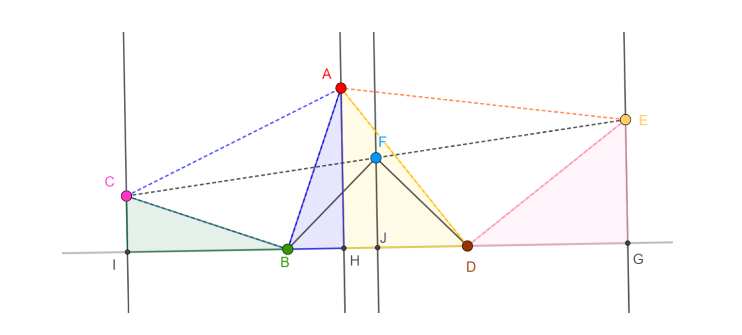
מורידים אנכים מ- E, A , C

משולשים DEG ו- ADH  חופפים ולכן מקבלים ש- EG = HD 

משולשים AHB ו- BIC חופפים ולכן מקבלים ש-  CI=BH

כלומר :  EG+CI = BD

נתון ש- F (מאגר המים) אמצע CE

נסמן את אמצע הקטע IG ב- J , נקבל ש- FJ קטע אמצעים בטרפז CIGE 

קטע אמצעים בטרפז מקביל לבסיסים ולכן מקבלים ש FJ מאונך ל- IG

התוצאה: FJ הוא אנך אמצעי במשולש BDF  .

 בנוסף, מתקבל ש- FJ שווה אמצע BD  כלומר שמשולש BFD  הוא משולש שווה שוקיים וישר זווית.