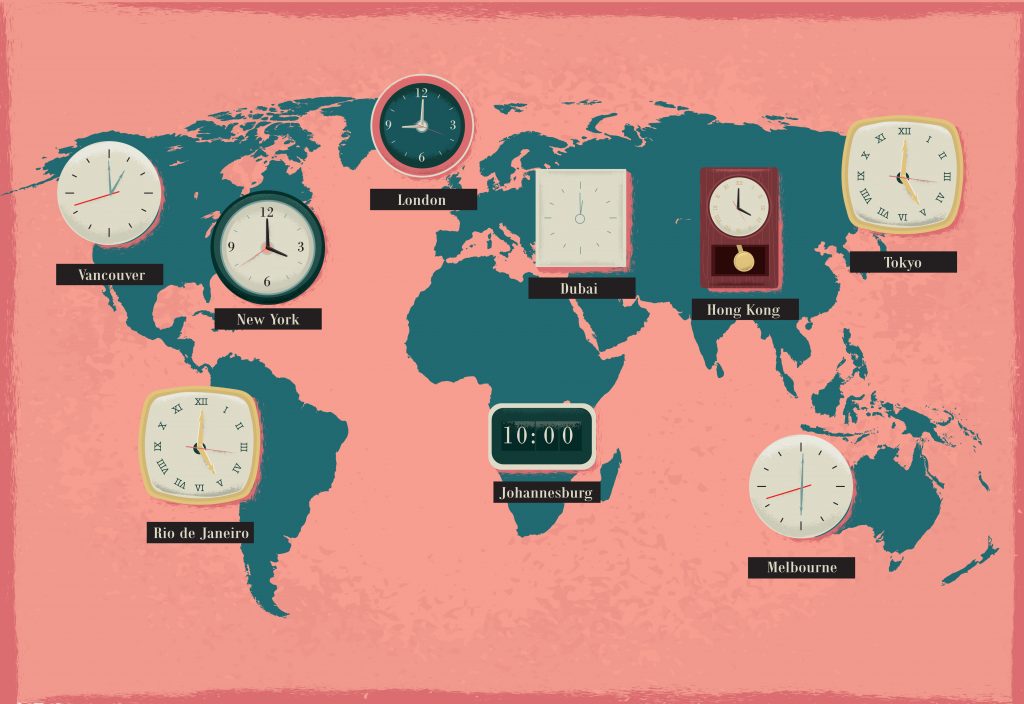
טורניר מקוון בינלאומי
משימה 1
המטרה של משימה זו היא לבדוק אם התלמיד יודע להשתמש בחיבור וחיסור מספרים מכוונים כדי למצוא פתרון לבעיה.
התלמיד מתבקש להגיש 3 דוגמאות שונות של איזורי זמן בהם יכולים להימצא מקום א ומקום ב. על מנת לעשות זאת, התלמיד צריך להבין שאותו מספר בשעון מחוגים יכול לייצג שעות שונות במהלך ה-24 שעות (למשל השעה 10 יכולה לייצג את השעה 10 בבוקר או 10 בלילה). לכן, ישנן שתי אפשרויות להסתכלות על ההפרש בין השעונים הנתונים:
אפשרות ראשונה שההפרש הוא 5 בכיוון השלילי (מוקדם יותר – במקרה זה השעונים מראים 3 לפנות בוקר ו- 10 בלילה יום לפני)
אפשרות שנייה שההפרש הוא 7 בכיוון החיובי (מאוחר יותר – במקרה זה השעונים מראים 3 אחרי צהריים ו- 10 בלילה באותו יום).
ישנה אפשרות לתלמיד להיעזר במפה שבפינה השמאלית של המסך.
https://en.wikipedia.org/wiki/Time_zone#/media/File:World_Time_Zones_Map.png
משימה 2:
המטרה של משימה זו היא לבדוק אם התלמיד מבין את נושא המחזוריות כך שאחרי 24 שעות התאריך משתנה (היממה היא בת 24 שעות).
במשימה זו נתונים אזורי הזמן של 4 מקומות על כדור הארץ, ונתונות טענות לגבי המספרים המופיעים בשעון הדיגטלי באותו הזמן בשניים מהמקומות הנתונים.
התלמיד מתבקש לבחור עבור כל טענה אם היא תמיד נכונה, לפעמים נכונה או אף פעם לא נכונה.
אם הטענה תמיד נכונה, התלמיד מתבקש להביא דוגמה שתומכת בטענה ע"י כתיבת השעה ובמידת הצורך כתיבת התאריך.
אם הטענה לפעמים נכונה התלמיד מתבקש להביא דוגמה אחת המדגימה מתי היא נכונה ודוגמה אחת המדגימה שאיננה נכונה.
אם הטענה לא נכונה אף פעם התלמיד מתבקש להסביר מדוע.
משימות 3+ 4 :
המטרה של משימות אלה היא לבדוק אם התלמיד מבין איך מרכיבים את הזוגות לפי שיקולים שונים: שיקולים לוגיים וחפיפה בזמנים שבהם המשחק יכול להתנהל.
(משימה 4 עוסקת בשיקולים לוגיים יותר מורכבים מאשר משימה 3)
בשתי המשימות נתון כי תיערך תחרות בין שני שחקנים במשחק מחשב שאורכו שעה וחצי, ונתונה רשימת שחקנים מכל רחבי העולם שעלו לרבע הגמר, כך שהיא מורכבת מ- 4 שחקנים בנים ו- 4 שחקניות בנות. בנוסף, נתון כי הזמנים בהם יכול להתקיים המשחק הם בין השעות 6:00- 9:00 או בין השעות 16:00 – 20:00 .
התלמיד מתבקש לבחור אלו מבין הטענות נכונות ואלו אינן נכונות.
אם הטענה נכונה, התלמיד מתבקש לכתוב את שמות כל השחקנים בכל זוג מתמודדים ולרשום באלו שעות הם יכולים לשחק.
אם הטענה לא נכונה, התלמיד מתבקש להסביר מדוע.
משימה 5:
המטרה של משימה זו היא לבדוק אם התלמיד יודע למצוא מתוך כל הצירופים האפשריים את אלה שיכולים לשחק כך שתהיה חפיפה בזמנים כאורך הזמן הנדרש למשחק.
במשימה זו נתוה טענה: "אחד המנהלים בתחרות הציע להרכיב משמונת המתמודדים שעלו לרבע הגמר ארבעה זוגות כך שכל זוג יכלול בן ובת. "
התלמיד מתבקש להחליט האם ההצעה ניתנת ליישום. אם כן, הוא מתבקש לרשום ארבעה זוגות של מתמודדים ברבע הגמר. אם לא, הוא מתבקש להסביר מדוע.
הרעיון בפעילויות מידול הוא שהתלמיד משלב ומשתמש בידע המתמטי שיש לו בכל מני נושאים, לפי השיקולים שלו, לכן פעילות זו עוסקת בכמה נושאים מתמטיים:
- נושא חישובי זמן שכולל מעבר בין שעון דיגיטלי ושעון אנלוגי (מחוגים), ייצוגים שונים לשעות, ומחזוריות של 24 (יממה). נושא זה נלמד בבית הספר היסודי (ראה עמוד 72 בתוכנית הלימודים של כיתה ג)
- נושא מספרים מכוונים שכולל חיבור וחיסור מספרים מכוונים תוך שימוש בישר המספרים. נושא זה נלמד בכיתה ז' (ראה עמוד 25 בתוכנית הלימודים של חט"ב)
- שימוש בכללי התאמה (פונקצית התאמה חיבור וחיסור של קבוע) לצורך פתרון הבעיה. נושא זה נלמד בכיתה ז' והעמקה בתחום זה נעשת בכיתה ח' (ראה עמוד 40 בתוכנית הלימודים של חט"ב)
- שימוש בידע שנלמד בכיתה ט' בהקשר להסתברות, על מציאת צירופים אפשריים, ויישומו לצורך פתרון בעיה בנושא אחר.
הנושאים המתמטיים שיכולים לעזור בפתרון הבעיה הם: חיבור וחיסור במספרים מכוונים, כללי התאמה, מציאת צירופים.
משימה 1
אחת הדרכים לפתרון הבעיה היא דרך הסתכלות על איזורי הזמן כשנתות של ציר ה-X כך ש- 0 מסמל את איזור הזמן של גריניץ': כל מה שבצד ימין הם איזורי זמן חיוביים וכל מה שבצד שמאל הם איזורי זמן שליליים.
ישנן כמה אפשרויות לפתרון:
אפשרות ראשונה שההפרש הוא 5 בכיוון השלילי (מוקדם יותר – במקרה זה השעונים מראים 3 לפנות בוקר ו- 10 בלילה יום לפני)
דוגמאות לפתרון: 2+ 3- , 1+ 4- , 1- 6-
אפשרות שנייה שההפרש הוא 7 בכיוון החיובי (מאוחר יותר – במקרה זה השעונים מראים 3 אחרי צהריים ו- 10 בלילה באותו יום).
דוגמאות לפתרון: 2+ 9+ , 1+ 8+ , 1- 6+
אפשרות שלישית:
אם התלמיד בוחר שאחד השעונים שייך לגריניץ' אז יש רק שתי אפשרויות לפתרון:
0 5- , 0 7+
משימה 2:

משימה 3:
ישנן כמה אפשרויות להרכבת זוגות:
- זוגות מעורבים (בן ובת בכל זוג): במקרה הזה אי אפשר לדעת מי יעלה לחצי הגמר.
- זוג אחד של שתי בנות וזוג של שני בנים, ו 2 זוגות מעורבים: במקרה הזה לפחות בת אחת תעלה לחצי הגמר אבל לא בטוח שהיא היחידה. דוגמא:

3. 2 זוגות של בנות ו-2 זוגות של בנים : במקרה הזה בוודאות יעלו שתי בנות לחצי הגמר. אבל לפי הנתונים במשימה, מריה לא יכולה לשחק עם עוד בת (אין חפיפה בין שעות המשחק שלהן).
משימה 4
משימה 5
דוגמא 1:
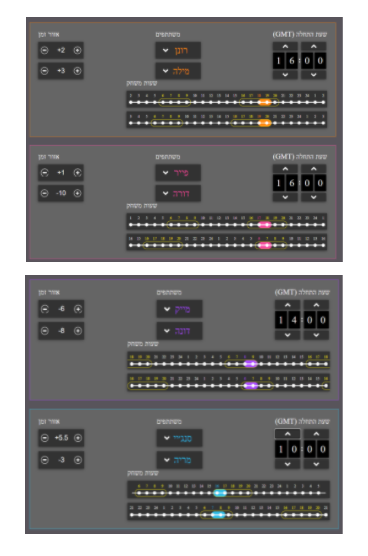
דוגמא 2:

בתהליך כתיבה
מה היתרון ומה החיסרון של כל אחד מהשעונים, שעון מחוגים ושעון דיגיטלי?
למה צריך את שני הייצוגים?
מתי כדאי להשתמש בכל ייצוג ?
משימה 5:
לדון על כל האפשרויות
האם יש קומבינציה/צירוף שהיא בלתי אפשרית?
האם ישנה בת ספציפית שלא יכולה לשחק עם כל הבנים?
אפשר להכין/לארגן את הנתונים בטבלה ולציין את כל הקומבינציות/הצירופים האפשרויות.