מטרת הפעילות הבנת משמעות פתרון המשוואה כערך ה x של נקודת המפגש של שני גרפים. בפעילות אין התייחסות לייצוג סימבולי (אלגברי) של משוואה.כל אגף מיוצג על ידי גרף של פונקציה קווית או ריבועית. 

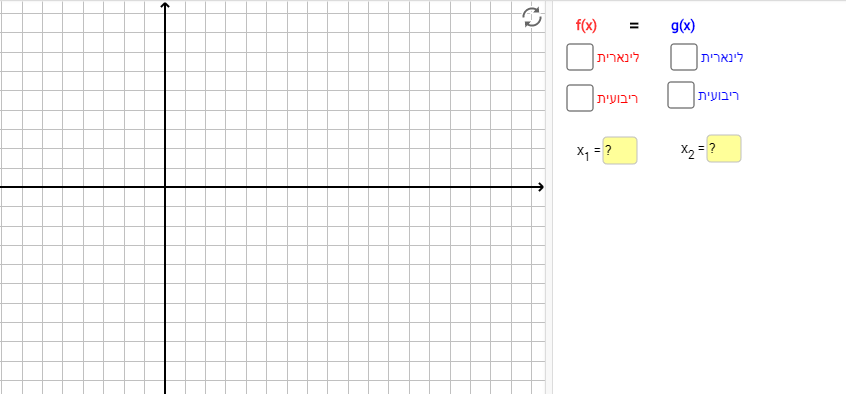
תלמידים מתבקשים לבחור פתרון של משוואה (על ידי כתיבת מספרים בתיבת טקסט), להחליט באיזה גרף הם משתמשים (קווי או ריבועי) ולגרור את הנקודות על הגרפים כך שהם ייצגו את הפתרון שנבחר. 

בפעילות  שלוש משימות:

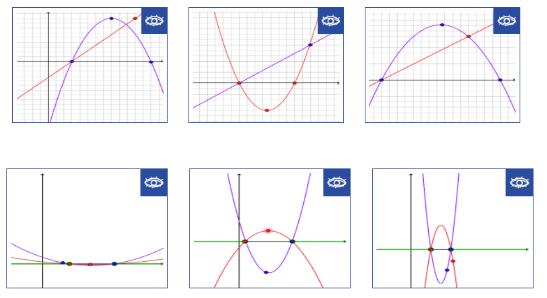
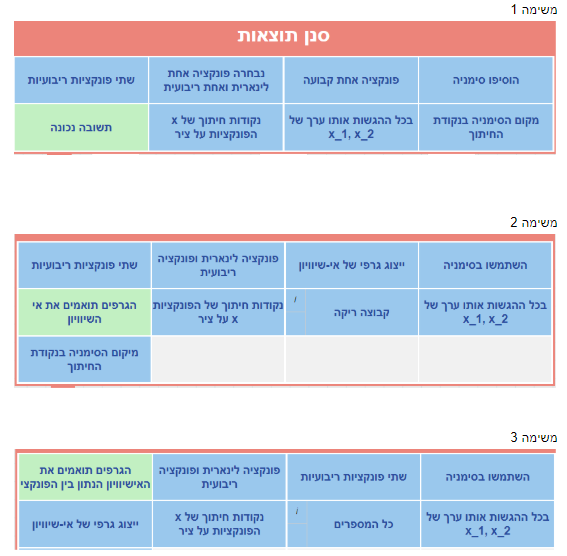
במשימה ראשונה תלמידים פותרים משוואה f(x)=g(x) בצורה גרפים 

במשימה השנייה תלמידים פותרים אי-שוויון f(x)<g(x) בצורה גרפים, כאשר פתרון האי-שוויון הוא מהצורה

x1<x<x2

במשימה השלישית תלמידים פותרים אי-שוויון  f(x)<g(x) בצורה גרפים כאשר פתרון האי-שוויון הוא מהצורה x<x1 או  x>x2

הפעילות מתאימה לקבוצות תלמידים הלומדים מתמטיקה ברמה גבוהה. היא משתלבת בתוכנית הלימודים של כיתה ט בנושא של פונקציה ריבועית, שיוויון ואי-שיוויון בין שתי פונקציות.

• את הייצוג הגרפי של פונקציה קווית וריבועית, 
• את משמעות ערך נקודות החיתוך כפתרון משוואה. 
• נדרש ידע בפתרון אי-שיוויון ריבועי.

תלמידים רבים ממקמים את נקודת חיתוך של שני גרפים על ציר ה x. חשוב להדגיש שפתרון של משוואה הוא למעשה הערך ה x של נקודת חיתוך ולכן חשוב להדגיש בדיון בכיתה שישנן אפשרויות רבות לגרפים המתאימים לפתרון הנבחר. במשימות 2 ו-3 אפשר לדון בקבוצת מספרים שנבחרה כפתרון לאישיווין. האם נבחרה קבוצה ריקה? האם נבחרה קבוצה של כל המספרים? האם ניתנה דוגמה תואמת לבחירת הנתונים. כדאי לשים לב אילו נתונים נבחרו על ידי התלמידים ומה הסיבה לבחירה זו.