לוחות וחותמות
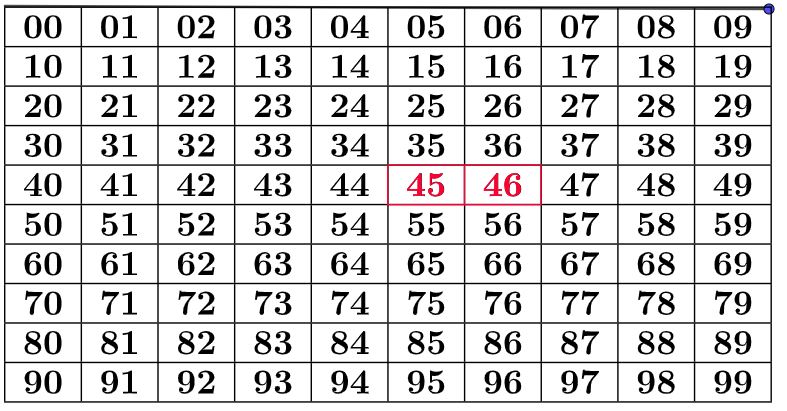
פעילות זו היא פעילות חקר העוסקת בהכללות וחוקיות בין מספרים מסודרים בלוח המורכב ממשבצות, כאשר בכל משבצת מוצב מספר.
המטרה היא לחקור ולמצוא חוקים מקומיים המקשרים בין המספרים בתוך חותמת נתונה – מבנה המורכב משתי משבצות.
קישור לכיתת התנסות
פעילות זאת פותחה על בסיס רעיונות מתוך פרויקט לוחות וחותמות בהובלת פרופ' מיכל ירושלמי.
בפעילות זו נתונים מספרים המסודרים בלוח המורכב ממשבצות, כאשר בכל משבצת מוצב מספר.
המספרים בלוח מסודרים בשורות, משמאל לימין.
כמו כן, נתונה חותמת – מבנה המורכב משתי משבצות – שניתן להזיז אותה באמצעות שני הסליידרים "ימינה/שמאלה" ו-"למעלה/למטה" בחלון הימני.

המטרה של פעילות זו היא לחקור ולמצוא חוקים מקומיים המקשרים בין המספרים בתוך החותמת.
הלוח יכול לשמש ככלי חקירה בנושאים שונים כמו הכללות, מושג המשתנה, היכרות ראשונה עם מושג הפונקציה, וסדרות.
מטרה נוספת היא לעודד את התלמידים לגלות צורות שונות של קשרים בין המספרים המופיעים בלוח ולנסח קשרים אלה באמצעות ביטויים ופונקציות.
משימה 1 עוסקת במספרים עוקבים שסכומם מתחלק ב-3.
התלמידים מתבקשים להניח את החותמת בשלושה מקומות שונים על גבי הלוח, כך שסכום שני המספרים המופיעים בה יתחלק ב-3.
ניתן להציג את הסכום של שני המספרים על ידי סימון הריבוע המתאים ביישומון.
משימה 2 עוסקת בזוגות של מספרים שספרת האחדות של סכומם היא אחד.
א- התלמידים מתבקשים להניח את החותמת בשלושה מקומות שונים על גבי הלוח, כך שספרת האחדות של סכום שני המספרים בה היא 1.
ב- התלמידים מתבקשים לענות על השאלה: האם קיימים זוגות של מספרים עוקבים המקיימים תכונה זו אך לא ניתן להניח את החותמת עליהם בלוח הנתון? הסבירו.
במשימה 3 נתונות טענות.
התלמידים מתבקשים לסמן את הטענות הנכונות, ולכל טענה נכונה להגיש דוגמה תומכת ע"י הזזת החותמת למקום המתאים.
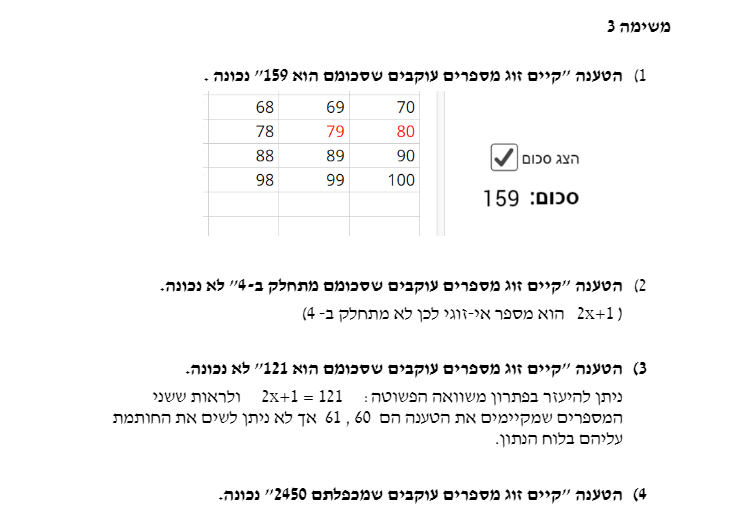
- קיים זוג מספרים עוקבים שסכומם הוא 159.
- קיים זוג מספרים עוקבים שסכומם מתחלק ב-4.
- קיים זוג מספרים עוקבים שסכומם הוא 121.
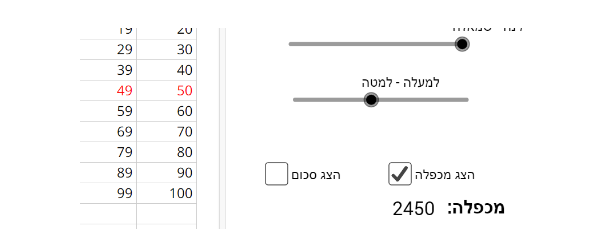
- קיים זוג מספרים עוקבים שמכפלתם 2450.
- 5. קיים מספר שאם נכפול אותו ב-6 ונחלק את המכפלה במספר העוקב נקבל 5.5
ניתן להציג את הסכום של שני המספרים ואת המכפלה שלהם על ידי סימון הריבוע המתאים.
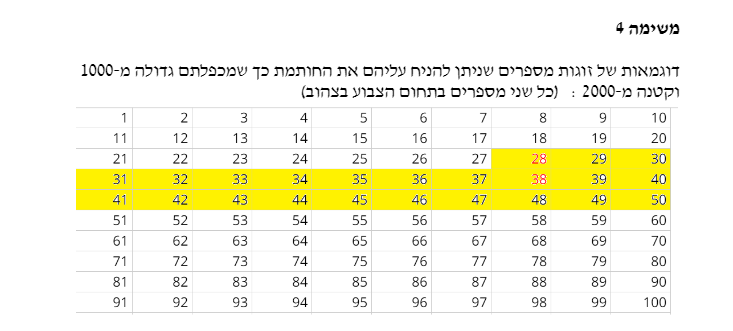
במשימה 4 נתונה חותמת המורכבת משתי משבצות אחת מעל השנייה.
ניתן להזיז את החותמת באמצעות שני הסליידרים "ימינה/שמאלה" ו-"למעלה/למטה", ולהציג את סכום שני המספרים המופיעים בחותמת או להציג את מכפלתם באמצעות סימון הריבוע המתאים בחלון הימני.
התלמידים מתבקשים להגיש שלוש דוגמאות של זוגות מספרים שניתן להניח עליהם את החותמת כך שמכפלתם גדולה מ-1000 וקטנה מ-2000

הנושאים "חוקיות", "משוואות ופתרונן" ו- "אי-שוויונות" נלמדים בכיתה ז'.
לפי תוכנית הלימודים "מוצע להציג את המושג 'משתנה' בדוגמאות שבהן רואים את התועלת שבו, למשל, תיאור מצבים חשבוניים והכללות של מקרים פרטיים (ניסוח חוקיות)". כמו כן, "יש לעסוק במגוון מצבים וסוגים שונים של חוקיות" (מתוך תוכנית הלימודים – עמ' 5)
כמו כן, לפי תוכנית הלימודים "יש לשים דגש על הבנת מושגי המשוואה ופתרונה" ובנוסף "מומלץ ללמד דרכי פתרון המצריכות מיומנויות בסיסיות בלבד".
לכן הפעילות מתאימה לכיתה ז', כפעילות חקר או כפעילות מסכמת לנושאים אלה.
פעולות החשבון
כתיבת ביטויים אלגבריים פשוטים
כתיבת ופתרון משוואה פשוטה עם נעלם אחד
משימה 1
כל זוגות המספרים שהסכום שלהם מתחלק ב- 3 :


5. הטענה "קיים מספר שאם נכפול אותו ב-6 ונחלק את המכפלה במספר העוקב נקבל 5.5 " נכונה.
שני המספרים שמקיימים את הטענה הם: 11 ו- 12 .
בתהליך כתיבה
משימה 1
- מה מאפיין את זוגות מספרים שהסכום שלהם מתחלק ב- 3?
- כמה אפשרויות שונות יש?
משימה 2
- מה מאפיין את זוגות המספרים המקיימים את הטענה? (אחד מהם עם ספרת אחדות 5, והשני עם ספרת אחדות 6)
- בסעיף ב, כדאי לדון עם התלמידים שישנם עוד אפשרויות לזוגות מספרים עוקבים וספרת האחדות בסכומם היא 1, אך לא ניתן לשים את החותמת עליהם (אחד מהם הוא עשרת שלמה והמספר השני הוא המספר העוקב, למשל: 40 + 41 )
משימה 3
- טענה 1: האם יש חוקיות מסוימת בין זוגות המספרים המקיימים את הטענה? איך מזהים שמספר מתחלק ב- 3 ללא שארית?
- טענה 2: כדאי לדון עם התלמידים למה הטענה לא נכונה (כי סכום כל שני מספרים עוקבים הוא מספר אי-זוגי ולכן לא מתחלק ב- 4). אפשר להיעזר בכתיבת הביטוי: 4 \( 2x+1)
- טענה 3 : חשוב לחדד לתלמידים ששני המספרים המקיימים את הטענה הם 60 ו- 61, אך לא ניתן לשים את החותמת עליהם בלוח הנתון כי כל אחד נמצא בשורה.
- טענה 4: כדאי לדון עם התלמידים באיך מוצאים את זוג המספרים העוקבים שמכפלתם היא 2450. ניתן להיעזר בצמצום אפשרויות ע"י הסתכלות על העמודות 9 ו- 10 או העמודות 4 ו- 5.
- טענה 5: ניתן לנסח עם התלמידים משוואה פשוטה שבעזרתה ניתן לפתור את השאלה:
6x/(x+1)=5.5
6x=5.5x+5.5
0.5x=5.5
x=11
משימה 4
- מה הן כל האפשרויות של זוגות מספרים המקיימים את הטענה?
- מה הוא תחום המספרים המקיימים את הטענה ?







