מושגים בגיאומטריה- משולש שווה שוקיים

בפעילות זו ניצור משולשים שווי שוקיים בעזרת סרטוט דינמי, נבדוק האם המשולשים שיצרנו הינם שווי שוקיים על ידי הצגת אזורי התשובות האפשריות. ההתנסות ביישומון מאפשרת להיחשף למגוון דוגמאות של משולשים ובעקבות כך להגיע להכללה מה מאפיין משולשים אלה.
קישור לכיתת התנסות
במשימה זו אנו מתמקדים במשולש שווה שוקיים, משולש שיש בו שתי צלעות שוות באורכן. שתי הצלעות השוות במשולש שווה-שוקיים נקראות שוקיים והצלע השלישית נקראת בסיס. הבסיס יכול להיות ארוך, קצר או שווה באורכו לשוקי המשולש. יש לשים לב שכאשר הבסיס שווה לשוקיים אז המשולש הינו שווה צלעות. משולש שווה צלעות הוא מקרה פרטי של משולש שווה שוקיים.
מטרות משימה זו הן להתנסות ביצירת דוגמאות רבות של משולשים שווה שוקיים כדי להגדיל את מרחב הדוגמאות מעבר לדוגמה האבטיפוסית המוכרת ולהגיע להכללה לגבי המאפיינים של משולשים אלה.
על התלמיד לגרור את קודקוד A וליצור משולשים שווי שוקיים. בהמשך, הוא יכול לבחון את מרחב התשובות שהשיב, ביחס למרחב התשובות הנכונות. במהלך הפעילות, התלמיד מתנסה ביצירת דוגמאות שונות למשולשים שווי שוקיים, בזיהוי המאפיינים ובעריכת הכללה לגבי משולשים אלו.
כדי לעודד את הילדים להתנסות ביישומון ולעורר דיון בתכנים העולים ממנו, אפשר לשאול:
- האם קיימות תשובות אפשריות נוספות מעבר למשולשים שיצרתם?
- מה נחשבת כתשובה נכונה? מה נחשב כתשובה לא נכונה?
- מה ניתן ללמוד על משולשים שווה שוקיים?
לאחר שהתלמידים מגישים את המשימה למורה הם יכולים לבצע הערכה עצמית ולצפות בכלל התשובות שהשיבו בעזרת לחיצה על הלחצן "צפייה במשוב". התבוננות בתשובות אלו, בהכוונה מתאימה, יכולה לעודד את התלמידים לערוך הכללה ביחס למשולשים שווי שוקיים. שימו לב, כל נקודה כחולה במשוב מסמנת את המיקום אליו נגרר קודקוד A.
במצב של "צפייה במשוב" מופיע בצד הימני לחצן בחירה "משולשים שווי שוקיים". לחצן זה מאפשר לבדוק מהו אזור התשובות הנכונות. אזור זה הינו אזור שבו נוצרים משולשים שווה שוקיים והוא מסומן בצבע ירוק (איור 2), כלומר כאשר גוררים את קודקוד A לאיזור הירוק משולש ABC יהיה בהכרח משולש שווה שוקיים. יש לשים לב שקיים מקום שאינו מסומן באיזור התשובות הנכונות בשני המעגלים, מעין "חור". כאשר גוררים את קודקוד A למקום זה נוצר "משולש מנוון" הנראה כמו זווית שטוחה (איור 3).


בלחיצה על "משולשים שווי שוקיים" יפתחו אפשרויות לגבי משולשים שווי שוקיים בעלי מאפיין נוסף.
אפשרות א': משולש שווה שוקיים שהוא גם שווה צלעות. משולש שווה צלעות הינו תשובה נכונה עבור משימה זו כיוון שמשולש שווה צלעות הינו מקרה פרטי של משולש שווה שוקיים (כמפורט לעיל במדריך למורה). במשימה זו ניתן ליצור שני משולשים כאלה, הם מסומנים במשוב כנקודות כחולות על הקווים הירוקים (איור 4).
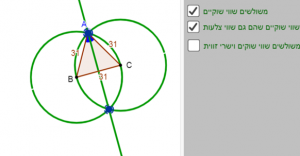
אפשרות ב': משולש שווה שוקיים שהוא גם ישר זווית. במשימה זו ניתן ליצור שישה משולשים כאלה. הם מסומנים במשוב כנקודות ירוקות (איור 5). יש לשים לב שכל אחת מהזוויות יכולה להיות זווית ישרה.

הערכה יחידנית
אוסף התשובות של תלמיד יחיד מופיעות כאוסף של נקודות כחולות. הצגת התשובות של תלמיד אחד מאפשרת למורה לזהות את התפיסות של התלמיד ולתמוך בו על פי הצורך.
דוגמה להערכה יחידנית: לפניכם תשובות שהגיש תלמיד עבור משימה זו (איור 6).
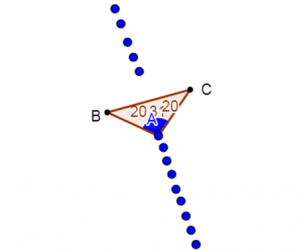
מתוך ביצועיו של תלמיד זה ניתן לראות שהוא יצר באופן עיקבי משולשים שווה שוקיים כך שהצלעות AC=AB. על אף שתשובותיו של תלמיד זה נכונות ניתן לקדם אותו ולשאול:
- האם ניתן ליצור משולשים שווה שוקיים כך שצלע AB או צלע AC היא בסיס המשולש?
- האם ניתן ליצור משולשים שווה שוקיים בעלי מאפיין נוסף (ישר זווית/קהה זווית)?
הערכה כיתתית:
הצגת כלל התשובות של תלמידי הכיתה במסך אחד] מאפשרת למורה לקבל תמונה עדכנית על ידע התלמידים ועל מאפייני התפיסות שלהם. בהתאם למידע זה, מומלץ לערוך דיון כיתתי כדי לחדד סוגיות מעניינות שעלו בתשובות ולהתייחס לשגיאות אופייניות. כמו כן מידע זה מאפשר למורה לתכנן את המשך הלמידה של הנושא במהלך אותו שיעור או לאחריו.
הדיון והתייחסות המורה לתשובות התלמידים הינם גורם חשוב בגיבוש נורמות כיתתיות בביצוע משימות אלו. כדי ליצור שטף של תשובות וגמישות מחשבתית יש לעודד את התלמידים להגיש תשובות מגוונות הכוללות מקרים מיוחדים ולא להסתפק בדוגמת האבטיפוס הרגילה.
סוגיות שניתן להתייחס אליהן בדיון הכיתתי:
- רוב הדוגמאות מרוכזות סביב איזור מסוים (איור 7)
הנטייה הראשונית היא להגיע את הדוגמה הנוחה והקלה ביותר, כיוון שהמשימה דורשת 10 דוגמאות אז התלמיד צריך להתאמץ ולחפש דוגמאות נוספות. ישנם תלמידים גוררים מעט את הקודקוד כדי ליצור 10 דוגמאות ואינם מחפשים דוגמאות שונות מהותית. למשל, ישנה נטייה ליצור משולשים קרובים לתפיסת האבטיפוס, על כן יתכן ורוב הדוגמאות המוגשות יהיו משולשים בהם הצלעות AC= AB ואילו דוגמאות של משולשים בהם הצלעות BC=AB או לחלופין BC=AC תהיינה פחות נפוצות.

משולש שווה צלעות כמקרה פרטי של משולש שווה שוקיים בהתאם ליכולת הכיתה והתלמידים ניתן להתייחס ליחסי ההכלה בין שני סוגי המשולשים, לדון על הגדרתו של משולש שווה שוקיים כ"משולש בעל שתי צלעות שוות באורכן" ולהדגים כיצד משולש שווה צלעות מתאים להגדרה זו.







