משימה ראשונה:

משימה זו היא משימה מקדימה, והמטרה שלה היא להעריך את הידע של התלמידים לגבי מימדים המשפיעים על נפח תיבה. 

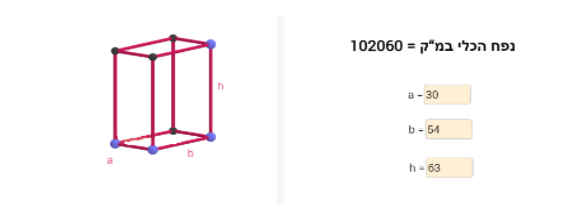
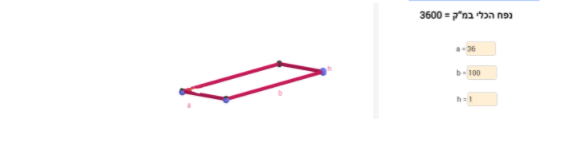
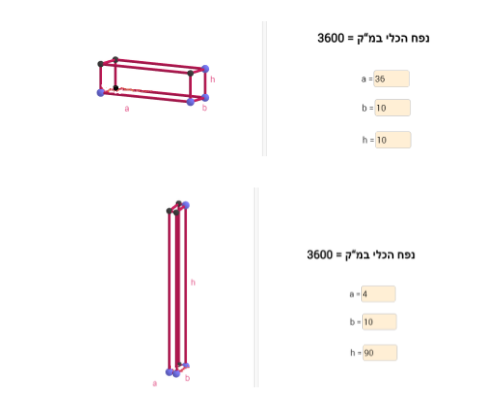
במשימה זו התלמיד מתבקש להגיש 3 דוגמאות של תיבות שונות כך שהנפח של כל אחת הוא 3600 מ"ק. 

המידות של התיבה נתונות במטרים.

כדי ליצור תיבה, ניתן לגרור את הנקודות הכחולות בסרטוט הדינאמי הנתון או להקליד אורכים מתאימים לקטעים המופיעים בחלון הימני שבישומון. 

משימה 2:

המטרה של משימה זו היא להעריך את הידע של התלמידים לגבי איזה מימדים של התיבה משפיעים על שיפוע גובה המים כתלות בזמן. 

במשימה זו נתונה תיבה אחת ולכן היא משימה מקדימה למשימה 3 שנתון בה שתי תיבות. 

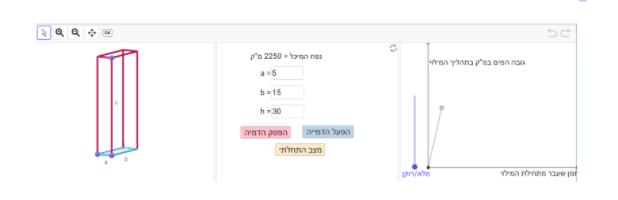
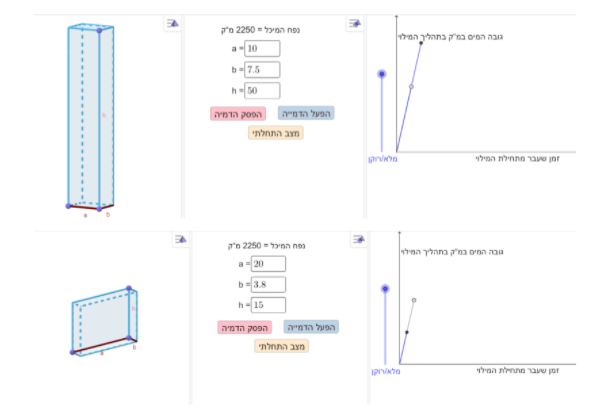
במשימה זו נתון מיכל מים בצורת תיבה שגובהה 30 מ', רוחבה 5 מ' ואורכה 15 מ'. כלומר שנפח המיכל הוא 2250 מ"ק.

הערה: הבסיס של התיבה הוא הפאה הצבועה בכחול (הגובה של המים המוזרמים).

כאשר מזרימים למיכל הזה מים בקצב קבוע נתון, מתקבל הגרף האפור בחלון הימני. גרף זה מתאר את גובה המים במיכל הנתון בהתאם לזמן שעבר מתחילת המילוי עד שהמיכל מתמלא במים.

הזרמת מים היא בקצב קבוע, כלומר שהגרף המתאר אותה הוא קו ישר כך שהשיפוע שלו משתנה בקטעי הזמן לפי מימדי הבסיס של התיבה.

התלמיד מתבקש ליצור מיכל ששונה במידותיו מהמיכל הנתון (a ו- b הם צלעות הבסיס, h הוא הגובה של התיבה), כך שאם יזרימו לתוכו מים באותו הקצב שבו הוזרמו המים למיכל הנתון: 

יתקבל גרף המתאר את גובה המים במיכל שלו בהתאם לזמן שעבר מתחילת המילוי שלו עד שהמיכל התמלא במים, בעל אותו שיפוע כמו הגרף האפור הנתון.

על התלמיד להגיש 3 דוגמאות שונות של מכלים העונים על הדרישה.

כדי ליצור מיכלים מתאימים, התלמיד יכול לשנות את מימדי המיכל בסרטוט הדינאמי על ידי גרירת הנקודות הכחולות או על ידי הקלדת הממדים המתאימים של המיכל.

שימו לב, האורך המקסימלי של כל צלע הוא 100 מטר.

כמו כן, בעזרת כפתור "הפעל הדמיה" ניתן למלא את המים במיכל ולראות את הגרף (צבוע בכחול) המתאר את גובה המים במיכל בהתאם לזמן שעבר מתחילת המילוי עד שהמיכל התמלא במים.

משימה 3

במשימה השנייה התלמידים מסיקים ששטח הבסיס של התיבה משפיע על שיפוע הגרף המתאר את גובה המים במיכל בהתאם לזמן שעבר מתחילת המילוי.  

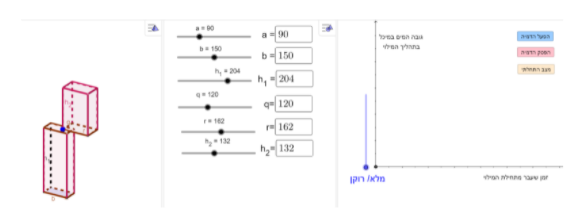
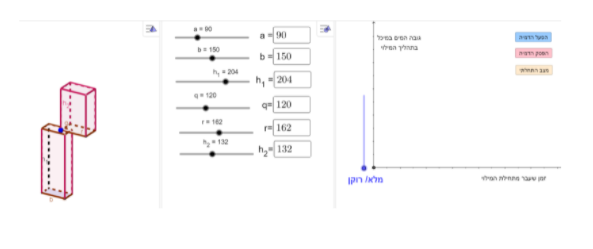
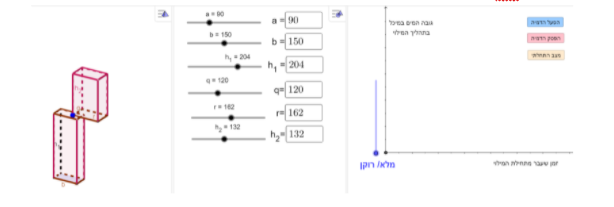
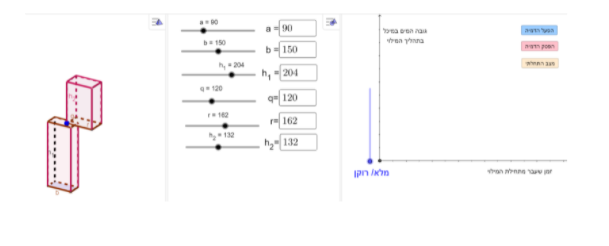
במשימה השלישית נתון מיכל לאגירת מים המורכב משתי תיבות המונחות זו על גבי זו, כך שלשתי התיבות חלק חלול משותף המאפשר למים המוזרמים לתיבה העליונה לעבור לתיבה התחתונה.

a ו- b הם צלעות הבסיס של התיבה התחתונה , h_1 הוא הגובה של התיבה התחתונה.

q ו- r הם צלעות הבסיס של התיבה העליונה , h_2 הוא הגובה של התיבה העליונה.

המידות של שתי התיבות נתונות במטרים.

לתוך המיכל הריק הזרימו מים בקצב קבוע עד שהמיכל התמלא.

התלמיד מתבקש להגיש 3 דוגמאות של מיכלים שונים כך שהגרף המתאר את גובה המים במיכל בהתאם לזמן שעבר מתחילת המילוי הוא קטע ישר.

אפשר לשנות את מימדי המיכל על ידי גרירת הסליידרים או על ידי הקלדת המימדים המתאימים של המיכל. שימו לב, האורך המקסימלי של כל צלע הוא 300 מטר.

כמו כן, בעזרת כפתור "הפעל הדמייה" אפשר למלא במים את המיכל ולראות את הגרף המתאר את גובה המים בהתאם לזמן שעבר מתחילת המילוי.

המטרה של המשימה הזו היא להעריך אם התלמידים מבינים ששטחי הבסיסים של שתי התיבות צריכים להיות שווים ולאו דווקא חופפים כדי לקבל שהגרף המתאר את גובה המים במיכל בהתאם לזמן שעבר מתחילת המילוי הוא קטע ישר, כלומר שני קטעים עם אותו שיפוע.

משימה 4 

במשימה הרביעית, התלמיד מתבקש להגיש 3 דוגמאות של מכלים שונים כך שהגרף המתאר את גובה המים במיכל בהתאם לזמן שעבר מתחילת המילוי מורכב משני קטעים כך ששיפוע הקטע הראשון גדול משיפוע הקטע השני.

המטרה של המשימה הזו היא להעריך אם התלמידים מבינים את היחסים בין שטחי הבסיסים של שתי התיבות ואת ההשפעה של שטח הבסיס על שיפוע הגרף המתאר את גובה המים במיכל (יחס הפוך: שטח בסיס קטן יותר יגרום לשיפוע ישר גדול יותר). 

משימה 5

המטרה של המשימה החמישית היא לבדוק אם התלמיד מבין איך המימדים השונים משפיעים על תכונות הגרף המתאר את גובה המים כתלות בזמן. 

הזרמת מים בקצב קבוע לשתי תיבות בעלות אותו נפח זה אומר אותו זמן מילוי לשתי התיבות. כלומר להבין שמה שמשפיע על הזמנים זה שהנפחים של התיבות צריכים להיות שווים (למלא באותה כמות מים).

שימו לב, קצב הזרמה קבוע לא אומר שהגרף שמתאר את גובה המים הוא קו ישר.

קצב הזרמה קבוע זה אומר שקצב השתנות הנפח הוא קבוע, כלומר שהגרף המתאר את קצב השתנות הנפח הוא קו ישר. 

במשימה זו, נתונות שלוש טענות. על התלמיד לבחור את הטענות הנכונות ולכל טענה נכונה להגיש דוגמה למיכל מתאים, כך שהגרף המתאר את גובה המים בו בהתאם לזמן שעבר מתחילת המילוי עד שהמיכל התמלא במים מורכב משני קטעים:

טענה 1:

קצב ההשתנות שלהם שונה וגובה המים בתיבה התחתונה שווה לגובה המים בתיבה העליונה. 

טענה 2:

קצב ההשתנות שלהם שונה וזמן המילוי של התיבה התחתונה שווה לזמן המילוי של התיבה העליונה. 

טענה 3:

קצב ההשתנות שלהם שונה, גובה המים בתיבה התחתונה שווה לגובה המים בתיבה העליונה וזמן המילוי של התיבה התחתונה שווה לזמן המילוי של התיבה העליונה.

משימה 6:

המטרה של משימה זו היא יישום של המסקנות שהתקבלו במשימה הקודמת. 

במשימה זו נתונות שתי טענות. על התלמיד להגיש דוגמה למיכל המתאים לכל טענה.

טענה 1: 

קיים מיכל כזה כך שהגרף המתאר את גובה המים בהתאם לזמן שעבר מתחילת המילוי עד שהמיכל התמלא במים מורכב משני קטעים שקצב ההשתנות שלהם שונה והיחס בין גובה המים בתיבה התחתונה לגובה המים בתיבה העליונה הוא 1:2.

טענה 2:

קיים מיכל כזה שהגרף המתאר את גובה המים במיכל בהתאם לזמן שעבר מתחילת המילוי עד שהמיכל התמלא במים מורכב משני קטעים שקצב ההשתנות שלהם שונה והיחס בין זמן המילוי של התיבה התחתונה גלזמן המילוי של התיבה העליונה הוא 2:1.

התלמידים מכירים את הגופים, ובפרט את התיבה, מבית הספר היסודי, ולומדים את נושא נפח תיבות בכיתה ז'. (ראה עמוד 20 בתוכנית הלימודים של חט"ב) 

נושא קריאת גרפים נלמד בכיתה ז', כך שלפי תוכנית הלימודים "יש להדגים תופעות המיוצגות באמצעות גרף במערכת צירים …… יש להציג את הגרף כתוספת לייצוגים אחרים שכבר נלמדו במהלך השנה" . (ראה עמוד 38 בתוכנית הלימודים של חט"ב) 

נושא קצב השתנות של פונקציה נלמד בסוף כיתה ז', כך שלפי תוכנית הלימודים "יש להדגים באמצעות טבלאות וגרפים כיצד פונקציה מתארת תופעה ….. צריך להבדיל בין השתנות בקצב אחיד לבין השתנות בקצב לא אחיד".(ראה עמוד 42 בתוכנית הלימודים של חט"ב) 

נושא יחס ופרופורציה נלמד בכיתה ח': "שני גדלים חיוביים משתנים, אשר היחס ביניהם קבוע, מקיימים יחס ישר", בדומה ליחס בין שטח בסיס התיבה לאורך אחת מצלעות הבסיס (הגדלת אחת מצלעות הבסיס פי 2 תגדיל את שטח הבסיס פי 2). 

דגומה נוספת לשימוש בנושא יחסים היא כשהגדלת אחד המימדים של התיבה פי 2 והקטנת מימד שני פי 2 לא ישנה את הנפח של התיבה.  (ראה עמוד 61 בתוכנית הלימודים של חט"ב) 

לכן, פעילות זו מתאימה כפעילות תרגול לכיתה ח' או ט' עבור תלמידים שלמדו את נושא נפח תיבה, קריאת גרפים וקצב השתנות של פונקציה קווית. 

חישוב נפח של תיבה. 

קריאת מידע מגרפים.

הבנת משמעות השיפוע של ישר. 

משימה 1: 

על מנת לקבל תיבות שנפחן הוא 3600 מ"ק, המכפלה של האורך ברוחב בגובה צריכה להיות 3600.  למשל:

משימה 2: 

במשימה זו התלמידים אמורים להגיע למסקנה שהשיפוע (של הגרף המתאר את גובה המים) לא מושפע מהגובה של התיבה, אלא משטח הבסיס ( כלומר מהרוחב ומהאורך של הבסיס). 

למשל:

משימה 3: 

כדי לקבל גרף המורכב משני קטעים עם אותו שיפוע (כלומר קו ישר אחד), שטחי הבסיסים של שתי התיבות צריכים להיות שווים. 

ישנם כמה מקרים שזה מתקיים:

תשובה טרוויאלית כאשר שתי התיבות שוות במימדים שלהן:

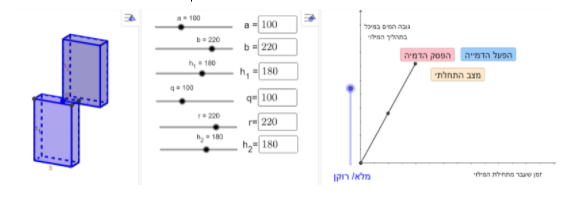
תשובה שבה שטחי בסיסים שווים אך הבסיסים לא חופפים:

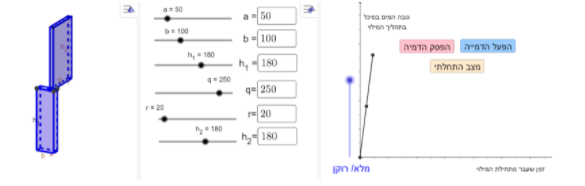
תשובה שבה שטחי בסיסים שווים וגם הבסיסים חופפים אבל לא מתלכדים (התיבה העליונה מוזזת):

תשובה שבה שטחי בסיסים שווים וגם הבסיסים חופפים ומתלכדים:

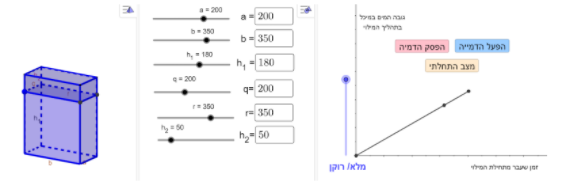
משימה 4: 

שיפוע הקטע הראשון גדול משיפוע הקטע השני מתקיים כאשר שטח הבסיס של התיבה התחתונה קטן יותר משטח הבסיס של התיבה העליונה. 

דוגמה: שטח הבסיס של התיבה התחתונה הוא 1000 מ"ק (100X100) ושטח הבסיס של התיבה העליונה הוא 6000 מ"ק (200X300).

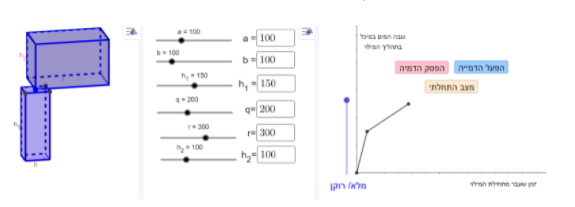
משימה 5

טענה 1:

כדי שקצב ההשתנות של התיבות יהיה שונה וגם גובה המים בתיבה התחתונה יהיה שווה לגובה המים בתיבה העליונה, צריך שגבהי התיבות יהיו שווים ושטחי הבסיסים יהיו שונים. למשל:

טענה 2:

כדי שקצב ההשתנות של התיבות יהיה שונה וגם זמן המילוי של התיבה התחתונה יהיה שווה לזמן המילוי של התיבה העליונה, צריך שנפחי התיבות יהיו שווים ושטחי הבסיסים יהיו שונים. למשל:

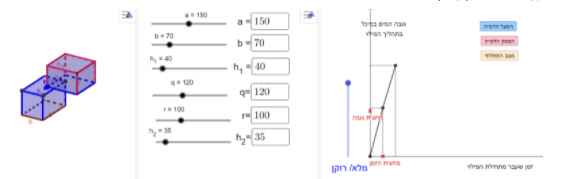
טענה 3: 

לא מתקיימת. 

גובה מים שווה זה אומר שגבהי התיבות צריכים להיות שווים, וזמן מילוי שווה זה אומר שנפחי התיבות צריכים להיות שווים. 

כדי ששני התנאים יתקיימו, שטחי הבסיסים של התיבות צריכים להיות שווים, זה אומר שקצב ההשתנות הוא שווה.

משימה 6

טענה 1: 

קצב ההשתנות שלהם שונה והיחס בין גובה המים בתיבה התחתונה לגובה המים בתיבה העליונה הוא 1:2 כלומר ששטחי הבסיסים לא שווים וגם הגבהים של התיבות הם ביחס 1:2. 

דוגמה: 

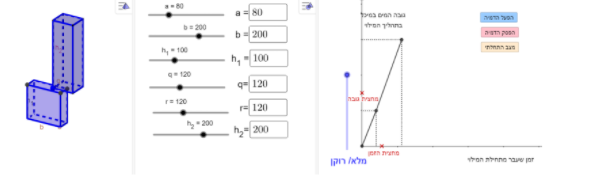
טענה 2: 

קצב ההשתנות שלהם שונה והיחס בין זמן המילוי של התיבה התחתונה לזמן המילוי של התיבה העליונה הוא 2:1 כלומר שנפח התיבה התחתונה גדול פי 2 מנפח התיבה העליונה, וגם שטחי הבסיסים לא שווים. 

דוגמה: 

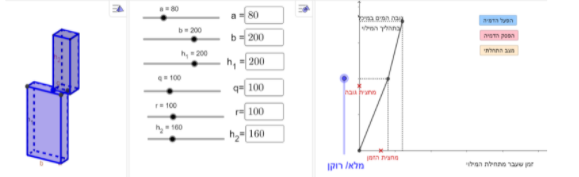
משימה 1: 

דרישות המשימה :

נפח התיבה הוא 3600 מ"ק 

מאפייני עבודה: 

הוזנו מספרים שלמים במימדי המיכל

שני מהמימדים הם כפולות של 10

הגובה הוא המימד הגדול ביותר 

הוגשה תיבה שהיא קובייה

הוגשה תיבה שהבסיס שלה הוא ריבוע

משימה 2:

דרישות המשימה: 

מימדי המיכל שונים ממימדי המיכל הנתון

שיפוע הגרף הכחול שווה לשיפוע הגרף האפור

מאפייני נכונות:

שטחי הבסיסים של שתי התיבות שווים

 מאפייני עבודה: 

גבהי שתי התיבות שונים 

הוזנו מספרים שלמים במימדי המיכל

נפח המיכל הוא 2250 מ"ק

משימה 3:

דרישות המשימה : 

שיפוע הגרף המתאר את גובה המים הוא קו ישר 

מאפייני נכונות:

שטחי הבסיסים שווים

הבסיסים של התיבות חופפים

הבסיסים של התיבות מתלכדים 

אותם מימדים של שתי התיבות

מאפייני עבודה: 

נפחי התיבות שווים

משימה 4:

דרישות המשימה: 

שיפוע הקטע הראשון גדול משיפוע הקטע השני

מאפיין נכונות:

שטח הבסיס של התיבה התחתונה קטן יותר משטח הבסיס של התיבה העליונה

מאפייני עבודה: 

הוגשה תיבה שבסיסה ריבוע 

גבהי שתי התיבות שווים

משימה 5:

מאפייני נכונות:

נבחרה הטענה הראשונה והוגשה דוגמה מתאימה 

נבחרה הטענה השנייה והוגשה דוגמה מתאימה 

טענה 1: קצב השתנות שונה 

                לשתי התיבות שטחי בסיס שונים

              גובה המים שווה בשתי התיבות

              לשתי התיבות אותו גובה 

טענה 2 :  קצב השתנות שונה 

               לשתי התיבות שטחי בסיס שונים

               זמן המילוי שווה לשתי התיבות

               לשתי התיבות אותו נפח

מאפייני עבודה: 

טענה 1: 

התיבות הזהות

לשתי התיבות אותו נפח 

טענה 2: 

התיבות הזהות

לשתי התיבות אותו גובה

משימה 6: 

דרישות המשימה:

הוגשה דוגמה מתאימה לטענה 1 

מאפייני נכונות:

קצב ההשתנות שונה 

שטחי הבסיסים לא שווים

היחס בין גובה המים בתיבה התחתונה לגובה המים בתיבה העליונה הוא 1:2 

גובה התיבה התחתונה קטן פי 2 מגובה התיבה העליונה 

דרישות המשימה:

הוגשה דוגמה מתאימה לטענה 2 

מאפייני נכונות:

קצב ההשתנות שלהם שונה 

שטחי הבסיסים לא שווים

היחס בין זמן המילוי של התיבה התחתונה לזמן המילוי של התיבה העליונה הוא 2:1 

נפח התיבה התחתונה גדול פי 2 מנפח התיבה העליונה

דוגמה לדיון:

• היישומון הנתון הוא בתלת מימד, לכן חשוב לסובב את התיבות, לראות את כל הכיוונים, מנקודות מבט שונים, כדי להבין יותר טוב. לפעמים כשמסתכלים מזווית מסויימת בתלת ממד רואים צורות בצורה ברורה יותר. דבר שלא מתאפשר בשרטוטים סטטיים בספרי הלימוד הרגילים.

משימה 1: 

• מה הם המימדים המשפיעים על נפח תיבה?
• כדאי לדון עם התלמידים שלא צריך כל פעם מחדש לחשוב על מידות חדשות שיוצרות את הנפח הרצוי, אלה ברגע שמוצאים מידות מתאימות אפשר להקטין ולהגדיל ביחס דומה את הגובה ואת צלעות הבסיס במטרה לשמור על אותו נפח. למשל אפשר להקטין את גובה התיבה פי 4 ומצד שני להגדיל את אחת מצלעות הבסיס פי 4 (או להגדיל כל צלע בבסיס פי 2). 

משימה 2: 

• איזה מימדים של התיבה משפיעים על שיפוע גובה המים כתלות בזמן?
• חשוב להדגיש שהזרמת מים היא בקצב קבוע, כלומר שהגרף המתאר אותה הוא קו ישר כך שהשיפוע שלו משתנה בקטעי הזמן לפי מימדי הבסיס של התיבה.

משימה 3: 

• חשוב לוודא שהתלמידים מבינים ששטחי הבסיסים של שתי התיבות צריכים להיות שווים ולאו דווקא חופפים כדי לקבל שהגרף המתאר את גובה המים במיכל בהתאם לזמן שעבר מתחילת המילוי הוא קטע ישר, כלומר שני קטעים עם אותו שיפוע.

• איך יראה הגרף של שינוי נפח המיכל כתלות בזמן ? (התשובה: קו ישר)
• מה ההבדל בין גרף המתאר את גובה המים כתלות בזמן לבין גרף המתאר את נפח המיכל כתלות בזמן? 

משימה 4:

• חשוב לוודא שהתלמידים מבינים את היחסים בין שטחי הבסיסים של שתי התיבות ואת ההשפעה של שטח הבסיס על שיפוע הגרף המתאר את גובה המים במיכל (יחס הפוך: שטח בסיס קטן יותר יגרום לשיפוע ישר גדול יותר). 

משימה 5:

• איך המימדים השונים משפיעים על תכונות הגרף המתאר את גובה המים כתלות בזמן?

• הזרמת מים בקצב קבוע לשתי תיבות בעלות אותו נפח זה אומר אותו זמן מילוי לשתי התיבות. כלומר להבין שמה שמשפיע על הזמנים זה שהנפחים של התיבות צריכים להיות שווים (למלא באותה כמות מים).

• שימו לב, קצב הזרמה קבוע לא אומר שהגרף שמתאר את גובה המים הוא קו ישר. קצב הזרמה קבוע זה אומר שקצב השתנות הנפח הוא קבוע, כלומר שהגרף המתאר את קצב השתנות הנפח הוא קו ישר. 
• למה טענה 3 לא מתקיימת אף פעם? 

גובה מים שווה זה אומר שגבהי התיבות צריכים להיות שווים, וזמן מילוי שווה זה אומר שנפחי התיבות צריכים להיות שווים. כדי ששני התנאים יתקיימו, שטחי הבסיסים של התיבות צריכים להיות שווים, זה אומר שקצב ההשתנות הוא שווה.

משימה 6: 

• קצב ההשתנות שונה כלומר ששטחי הבסיסים לא שווים
• היחס בין גובה המים בתיבה התחתונה לגובה המים בתיבה העליונה הוא 1:2 כלומר הגבהים של התיבות הם ביחס 1:2. 
• היחס בין זמן המילוי של התיבה התחתונה לזמן המילוי של התיבה העליונה הוא 2:1  כלומר שנפח התיבה התחתונה גדול פי 2 מנפח התיבה העליונה.