הפעילות עוסקת בייצוגים שונים של פונקציה קווית ופונקציה ריבועית (גרף, טבלה, מילולי), ובנוסף במשמעות שיפוע הגרף בתוך הסיפור הנתון (תיאור מילולי). 

בכל המשימות נתונים היגדים מילוליים כך שהתלמיד מתבקש להתאים להם גרפים ע"י שינוי הנתונים ביישומון. 

היישומון כולל ייצוג גרפי בעזרת נקודות, ייצוג טבלאי ואפשרות להצגת שיפוע הגרף בעזרת מדרגות.  

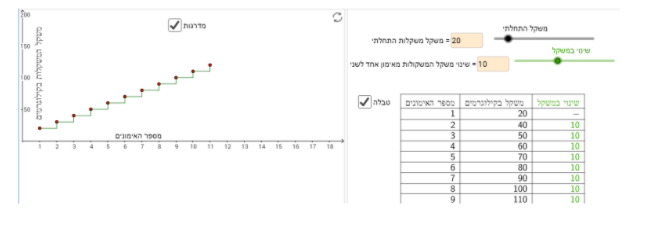
לכל המשימות נתון רקע: 

חדר כושר רכש מכונת הרמת משקולות חדשה ומתוחכמת.

המכונה יכולה לנהל תוכנית אימון בה משתנה משקל המשקולות מאימון אחד למשנהו.

הערות: ניתן להרים משקולות במשקל מקסימום פי 1.5 מהמשקל של אדם.

במשימה הראשונה התלמיד מתבקש להגיש 3 דוגמאות שונות לתוכנית אימון שבה מעלים את משקל המשקולות, כל אימון אותה תוספת משקל.

על התלמיד לשנות את הנתונים ביישומון כך שיתאימו לגרפים המתארים את תוכניות האימון השונות.

משימה זו היא משימה מקדימה, להיכרות עם הסיפור הכללי ולהתנסות עם היישומון והכלים המצורפים. 

במשימה השנייה נתונים 4 תיאורים. התלמיד מתבקש להכניס נתונים ביישומון ולהגיש דוגמא לתוכנית אימון לכל אחד מהתיאורים. 

המטרה של המשימה הזו היא לבדוק אם התלמיד מבין את המשמעות של הפרמטרים (משקל התחלתי, שינוי במשקל) בתוך הסיפור הנתון. 

המשימה השלישית והרביעית עוסקות בהבדל בין קצב שינוי קבוע לקצב שינוי משתנה. 

בשתי המשימות האלה, נוסף פרמטר שלישי "שינוי של השינוי" שבעזרתו ניתן להגיע לפונקציה ריבועית. 

במשימה השלישית התלמיד מתבקש לתת דוגמאות שונות לתוכנית אימון שבה מגיעים למשקל המקסימלי האפשרי.

במשימה הרביעית נתונות טענות, התלמיד מתבקש להתאים גרף מתאים לכל טענה. ישנן טענות המתייחסות לקצב שינוי קבוע וטענות המתייחסות לקצב שינוי משתנה.

במשימה החמישית נתונים 4 היגדים. כל היגד מתאר תוכניות אימון של שני מתאמנים.

התלמיד מתבקש לשנות את הנתונים ביישומון כך שיוצג גרף המתאים לתוכניות המתוארות בהיגד.

נושא השתנות של פונקציה נלמד בכיתה ז' כך שלפי תוכנית הלימודים "יש להדגים באמצעות טבלאות וגרפים כיצד פונקציה מתארת תופעה. מהכרת הפונקציה אפשר ללמוד על השתנות של תופעה….. ההשתנות של פונקציה באה לידי ביטוי בייצוג הגרפי במעבר מנקודה אחת על הגרף לנקודה אחרת עליו, ובשינוי של ערכי הפונקציה בין שתי הנקודות." 

בנוסף, בנושא השתנות של פונקציה בקצב אחיד ובקצב לא אחיד, תוכנית הלימודים מדגישה את הצורך בלהבדיל בין השתנות בקצב אחיד לבין השתנות בקצב לא אחיד, כשהפונקציה מיוצגת באמצעות טבלה או גרף.

" הביטוי הגרפי של קצב ההשתנות של הפונקציה הוא היחס שבין השינוי האנכי של הגרף לבין השינוי האופקי שלו. מקובל לכנות זאת קצב שינוי על פני מדרגה. גרף משתנה בקצב אחיד אם קצב השינוי הוא זהה על פני כל המדרגות, ובמקרה זה הגרף הוא קו ישר. בכל מקרה אחר, הגרף משתנה בקצב שאיננו אחיד."

אפשר להעביר את הפעילות כפעילות מקדימה לנושא פונקציות בכיתה ז', לתלמידים שלמדו נושא השתנות של פונקציה וקריאת גרפים, או לתלמידים בכיתות ח-ט אשר למדו את נושא הפונקציה הקווית. 

(ראה עמוד  42   בתוכנית הלימודים של חט"ב) 

קריאת גרפים

הבנת משמעות קצב שינוי קבוע ומשתנה 

משימה 1:

בדוגמה הזו ניתן לראות שהתלמיד בחר במשקל התחלתי 5 ק"ג והשינוי במשקל הוא 1.8 ק"ג מאימון לאימון. כמו כן, התלמיד נעזר בייצוג טבלה וגם בייצוג מדרגות. 

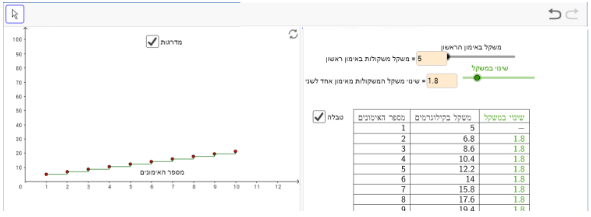
לעומתה, בדוגמה הבאה ניתן לראות שהתלמיד בחר במשקל התחלתי 30 ק"ג והשינוי הוא 5 ק"ג מאימון לאימון. כמו כן, ניתן לראות שהתלמיד לא נעזר בכלים השונים (טבלה ומדרגות).

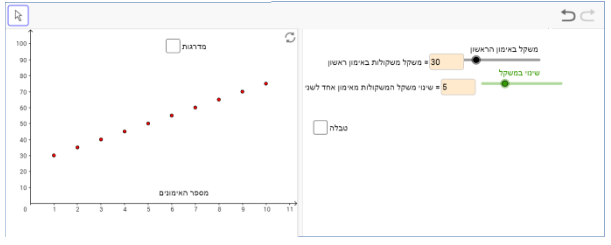
משימה 2:

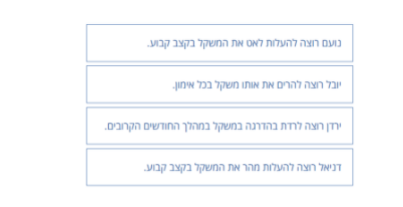
תיאור 1: נועם רוצה להעלות לאט את המשקל בקצב קבוע.

במקרה הזה, שינוי משקל המשקולות מאימון לאימון צריך להיות גדול מ- 0 (פונקציה עולה): 

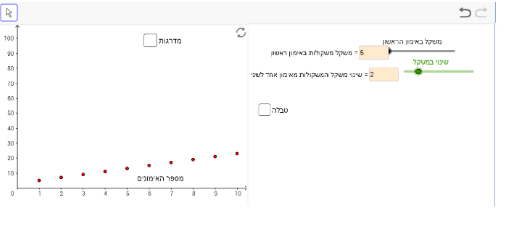
תיאור 2: יובל רוצה להרים את אותו משקל בכל אימון.

במקרה הזה, שינוי משקל המשקולות מאימון לאימון צריך להיות 0 (פונקציה קבועה):

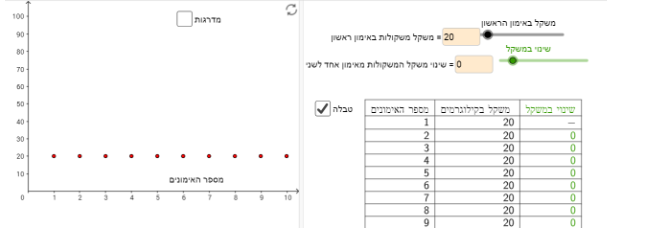
תיאור 3: ירדן רוצה לרדת בהדרגה במשקל במהלך החודשים הקרובים.

במקרה הזה, שינוי משקל המשקולות מאימון לאימון צריך להיות קטן מ- 0 (פונקציה יורדת):

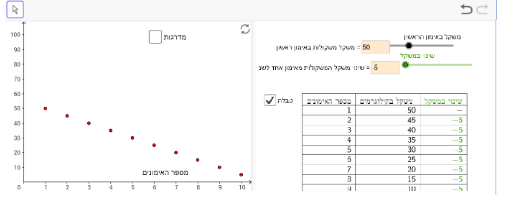
תיאור 4: דניאל רוצה להעלות מהר את המשקל בקצב קבוע.

במקרה הזה, שינוי משקל המשקולות מאימון לאימון צריך להיות גדול מ- 0 (פונקציה עולה), וגם גדול מהשינוי שהתלמיד בחר בתיאור הראשון:

למשל, סטודנט 11 בחר בתיאור הראשון שהשינוי הוא 1 ק"ג, ובתיאור הרביעי בחר שהשינוי הוא 6.5 ק"ג. 

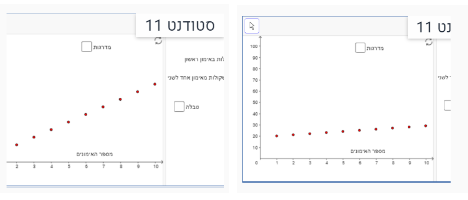
משימה 3:

דני שוקל 70 ק"ג, ולכן המשקל המקסימלי של המשקולות שהוא יכול להרים הוא 105 ק"ג (פי 1.5 מהמשקל שלו). 

דוגמה שבה השינוי בהתחלה קטן ואחר כך גדל:

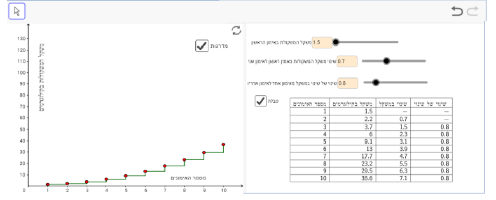
דוגמה שבה דני מגיע למשקל משקולות 104 ק"ג באימון ה- 10 (קרוב למשקל המקסימלי). 

במקרה הזה כדאי לדון עם התלמידים בשאלה "מה קורה אחרי האימון העשירי?"

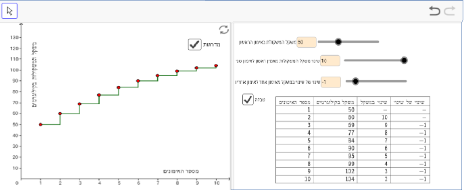
משימה 4:

תיאור 1: להעלות את המשקל בקצב קבוע ולהגיע למשקל גדול תוך זמן קצר.

במקרה הזה, פרמטר "השינוי של השינוי" צריך להיות 0 , ופרמטר "שינוי משקל מאימון ראשון לאימון שני" צריך להיות גדול מ-7 ק"ג, למשל: 

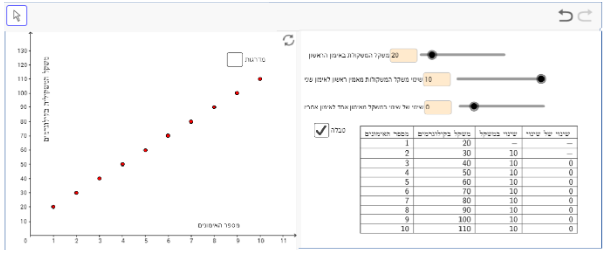
תיאור 2: להתחיל במשקל נמוך ולהעלות את המשקל במהירות.

משקל המשקולות ההתחלתי קטן מ- 20 ק"ג, ופרמטר "השינוי של השינוי" גדול מ- 0:

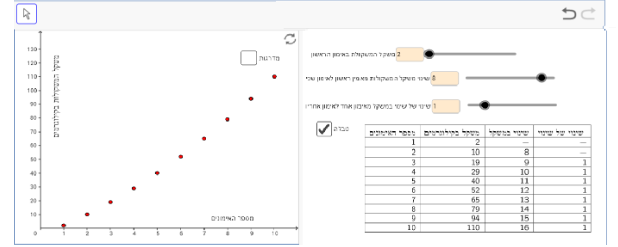
תיאור 3: בתחילת האימונים להוריד את המשקל ואחר כך להעלות במהירות

במקרה הזה, פרמטר "השינוי של השינוי" צריך להיות גדול מ- 0 , ופרמטר "שינוי משקל מאימון ראשון לאימון שני" צריך להיות קטן מ- 0, למשל: 

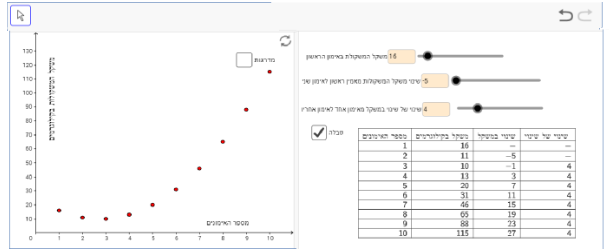
תיאור 4: להעלות לאט את המשקל בקצב קבוע.

במקרה הזה, פרמטר "השינוי של השינוי" צריך להיות 0 , ופרמטר "שינוי משקל מאימון ראשון לאימון שני" צריך להיות קטן מ- 7, למשל: 

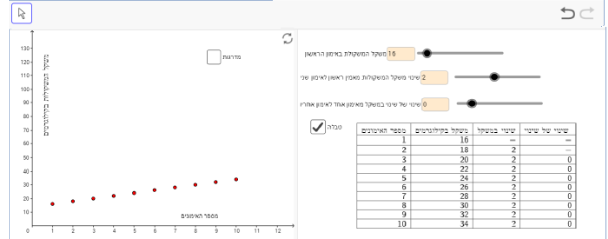
משימה 5:

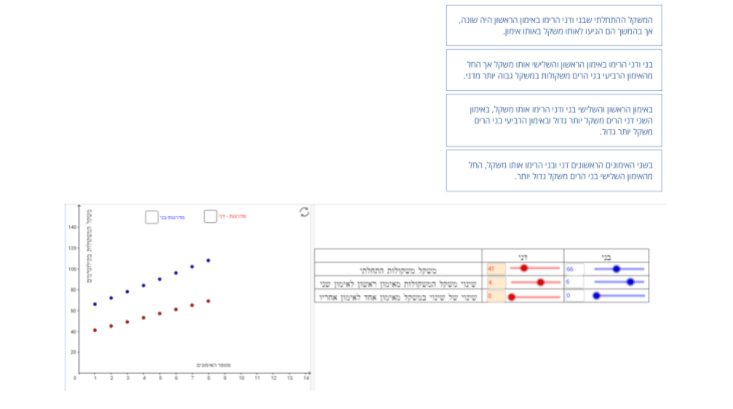
תיאור 1: באימון הראשון בני ודנה הרימו אותו משקל, וגם באימון השני הרימו אותו משקל, אך החל מהאימון השלישי בני הרים משקל גדול יותר.

בדוגמה הזו, באימון הראשון בני ודנה הרימו אותו משקל 15 ק"ג, גם באימון השני הרימו אותו משקל 18 ק"ג, והחל מהאימון השלישי בני הרים משקל גדול יותר.

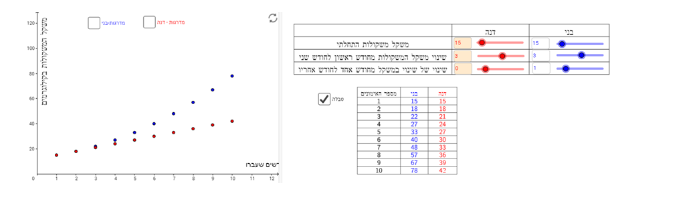
תיאור 2: באימון הראשון בני ודנה הרימו אותו משקל, וגם באימון השלישי הרימו אותו משקל, אך החל מהאימון הרביעי בני הרים משקולות במשקל גבוה יותר מדנה.

בדוגמה הזו, באימון הראשון בני ודנה הרימו אותו משקל 10 ק"ג, גם באימון השלישי הרימו אותו משקל 22 ק"ג, והחל מהאימון הרביעי בני הרים משקולות במשקל גבוה יותר מדנה.  

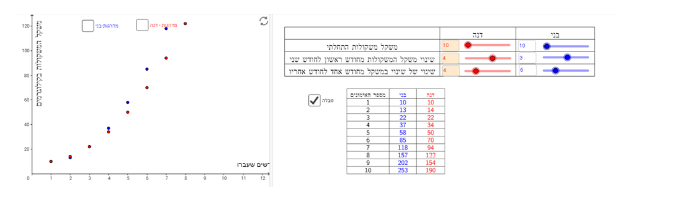
תיאור 3: באימון הראשון בני ודנה הרימו אותו משקל, וגם באימון השלישי הרימו אותו משקל. באימון השני דנה הרימה משקל יותר גדול ובאימון הרביעי בני הרים משקל יותר גדול.

בדוגמה הזו, באימון הראשון גם דנה וגם בני הרימו 5 ק"ג, באימון השלישי גם דנה וגם בני הרימו 15 ק"ג, באימון השני דנה הרימה 15 ק"ג ובני הרים 9.5 ק"ג, ובאימון הרביעי בני הרים 21.5 ק"ג ודנה הרימה 5 ק"ג. 

(שימו לב, יש לדון עם התלמידים במה קורה עם דנה אחרי האימון ה-4)

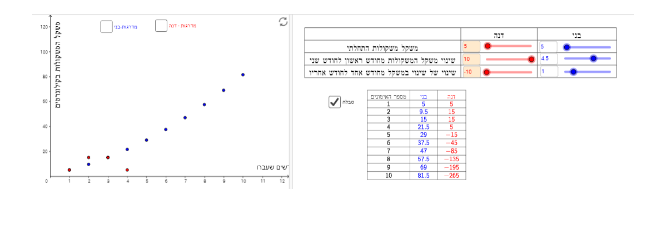
תיאור 4: המשקל ההתחלתי שבני ודנה הרימו באימון הראשון היה שונה, אך בהמשך הם הגיעו לאותו משקל באותו אימון.

בדוגמה הזו, באימון הראשון דנה הרימה 12 ק"ג ובני הרים 2 ק"ג, ושניהם הגיעו לאותו משקל משקולות באימון ה-6. 

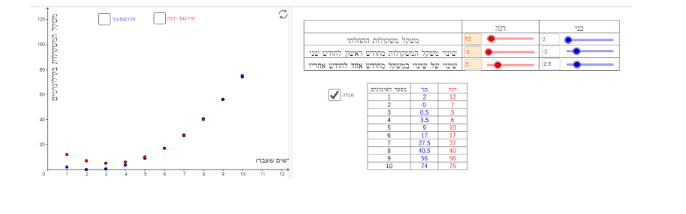
משימה 1:

ייצוג של מדרגות

ייצוג של טבלה

המשקל ההתחלתי גדול מ 80 ק"ג

המשקל ההתחלתי קטן מ 5 ק"ג

לא היה שינוי במשקל

שינוי במשקל שלילי

משימה 2:

ייצוג של מדרגות

ייצוג של טבלה

שינוי קטן במשקל בתוכנית של נועם

אין שינוי במשקל בתוכנית של יובל

יש ירידה במשקל בתוכנית של ירדן

עליה מהירה במשקל בתוכנית של דניאל

משימה 3:

ייצוג של מדרגות

ייצוג של טבלה

המשקל ההתחלתי קטן מ 5 ק"ג

המשקל ההתחלתי גדול מ 80 ק"ג

לא היה שינוי במשקל מאימון אחד ואימון אחר

השינוי במשקל קבוע

השינוי במשקל שלילי

השינוי בהתחלה קטן ואחר כך גדל

משימה 4:

ייצוג של מדרגות

ייצוג של טבלה

הגדיל את המשקל בקצב קבוע והגיע למשקל גדול תוך זמן קצר

התחיל במשקל נמוך והעלה את המשקל במהירות

עלייה לאט במשקל בקצב קבוע

בתחילת האימונים הוריד את המשקל ואחר כך העלה במהירות

משימה 5:

המשקל באימון הראשון היה שונה

הגיעו לאותו משקל באותו אימון

המשקל ההתחלתי שבני ודני הרימו באימון הראשון היה שונה, אך בהמשך הם הגיעו לאותו משקל באותו אימון.

באימון ראשון דני ובני הרימו אותו משקל

באימון השלישי דני ובני הרימו אותו משקל

החל מהאימון הרביעי בני הרים משקולות במשקל גדול יותר מדני

בני ודני הרימו באימון הראשון והשלישי אותו משקל אך החל מהאימון הרביעי בני הרים משקולות במשקל גבוה יותר מדני.

באימון השני דני הרים משקל גדול יותר מבני

באימון הרביעי בני הרים משקל יותר גדול מדני

באימון הראשון והשלישי בני ודני הרימו אותו משקל, באימון השני דני הרים משקל יותר גדול ובאימון הרביעי בני הרים משקל יותר גדול.

החל מהאימון השלישי בני הרים משקל גדול יותר

בשני האימונים הראשונים דני ובני הרימו אותו משקל, החל מהאימון השלישי בני הרים משקל גדול יותר.

משימה 1:

• יש לדון במשמעות הערכים שהתלמידים הכניסו. למשל שינוי משקל גדול מאוד (לא מציאותי) או משקל שלילי (מה זה אומר?)
• יש לדון עם התלמידים לגבי השיקולים לשימוש בייצוגים השונים: המדרגות בגרף (מייצגות את השינוי בקצב), טבלת ערכים, ייצוג גרפי. מתי כל אחד מועיל ורלוונטי.
• יש לדון עם התלמידים למה הגרף הוא גרף נקודות ולא קו ישר. והאם לכל נקודה על גרף הפונקציה – בהכרח יש משמעות במציאות.

משימה 2:

• יש לדון במשמעות של שני הפרמטרים ובמשמעות הערכים השונים (ערכים שליליים, 0 , ערכים חיוביים).
• אפשר לקשר בין התיאורים המילוליים הנתונים לבין הפרמטרים (b, m ) שהתלמידים מכירים במשוואת פונקציה קוית. 
• יש לדון בהבדל בין קצב שינוי לינארי לעומת מעריכי.
•  

משימה 3: 

• יש לדון במשמעות שלושת הפרמטרים והערכים השונים שלהם (שקובעים את סוג הפונקציה: קבועה, קווית, ריבועית)
• ניתן להתייחס לעניין המשך האימונים, כלומר מה קורה אחרי האימון העשירי לפי הערכים שהוזנו.

• אם רוצים להעלות את רמת הדיון – אפשר להגיע לביטוי האלגברי המתאים לגרף ע"י חישובים.

משימה 4:

• האם התלמידים לקחו בחשבון בתשובות שלהם את הנתון שהמשקל המקסימלי שניתן להרים הוא בערך 1.5 ממשקל האדם?
• מה סוג נקודת הקיצון במקרה המתואר? ומה קורה באימונים העוקבים?

משימה 5:

• לפי הגרפים – בלי השימוש בטבלה – איך יודעים שבאותו אימון הם הרימו אותו משקל? (נקודות מתלכדות)