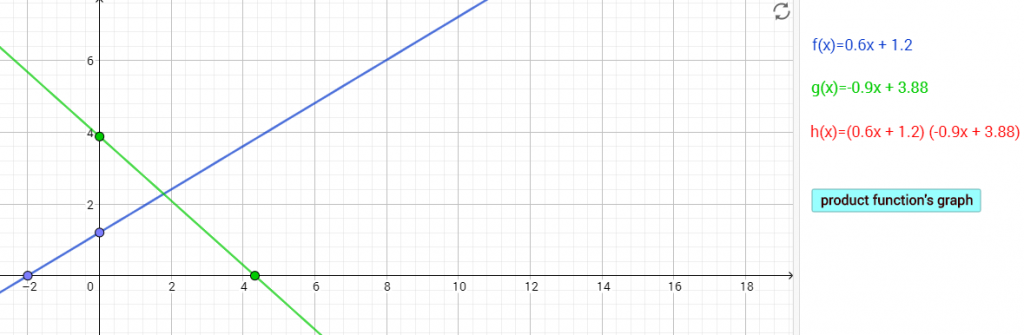
מטרת הפעילות היא הכרה של פונקציה ריבועית כמכפלה של שתי פונקציות קוויות (שאינן קבועות). בפעילות שתי משימות זהות במטרה שהתלמידים ייגישו בתחילה את המשימה הראשונה, יקבלו משוב על דוגמאות שהם הגישו וישנו/ או לא ישנו את הדוגמאות בהגשה חוזרת במשימה שניה. מטרה נוספת של הפעילות היא לבצע חקר סביב תופעה מתמטית המעודדת העלאת השערות והצדקות.

הנושא של פונקציה ריבועית נלמד בדרך כלל בכיתות ט. הפעילות מתאימה כפעילות פתיחה בנושא של פונקציה ריבועית, פעילות העשרה בכיתה ט מדעית או פעילות בנושא של גיאומטריה אנליטית בכיתות י-יא.

• שיפוע של פונקציה קווית
• משמעות נקודות על הצירים
• גרף שעובר בנקודות נתונות
• סוגי גרפים של פונקציה ריבועית (פרבולות)

• האם היה שימוש בכפתור ייצור גרף הפונקציה 
• פרבולה ישרה
• פרבולה הפוכה
• שימוש בפונקציה קבועה
• שתי פונקציות קוויות עם שיפוע חיובי
• שתי פונקציות קוויות עם שיפוע שלילי
• שתי פונקציות קוויות עם שיפועים מנוגדים
• פרבולה משיקה לציר ה-x
• פונקציות מקבילות
• פונקציות נחתכות
• פרבולה סימטרית ביחס לציר ה-y
• פונקציות קוויות נחתכות על ציר ה-y.

פעילות זו יכולה להיות פעילות הכרה עם פונקציה ריבועית. אפשר להדגיש מספר נקודות:

• פונקציית מכפלה של שתי פונקציות קוויות היא פונקציה ריבועית. יש לשים לב כי המקרים של פונקציות קוויות קבועות אינן נכללים במשימה, אך ניתן להעלות את המקרים האלה לדיון.
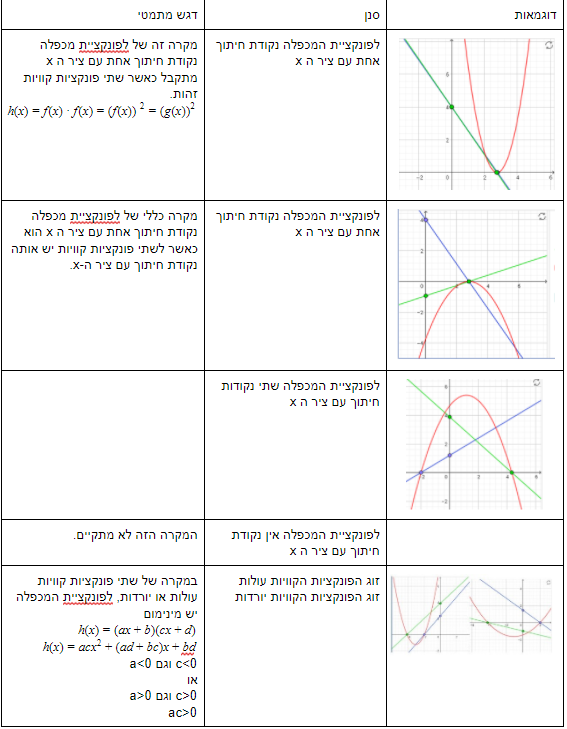
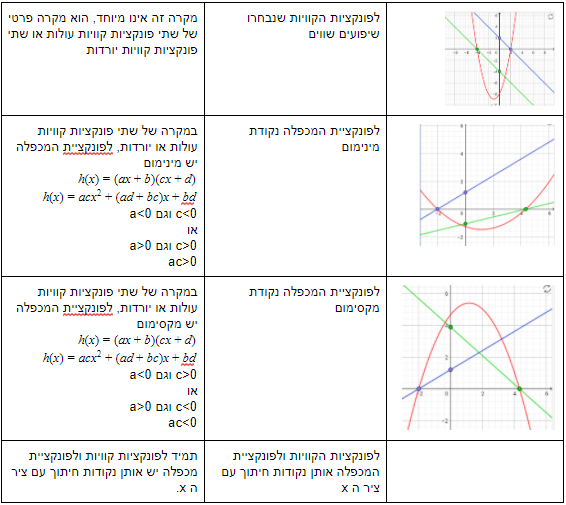
• ישנם פרבולות שונות – עם מקסימום, עם מינימום. ניתן לזהות קשר בין שיפועים של פונקציות קוויות ומינימום ומקסימום של פרבולות.
• חשוב לדון בשני תנאים: אחד שמתקיים תמיד (לשתי פונקציות קוויות ולפונקציית הכפלה יש אותן נקודות חיתוך עם ציר ה x) ואחד שלא מתקיים אף פעם (לפונקציית המכפלה אין נקודת חיתוך עם ציר ה x). נקודה לדיון: האם קיימות פרבולות שאין להן נקודות חיתוך עם ציר ה x? אם כן, מדוע במשימה זו לא ניתן לקבל פרבולות מסוג זה? 

האם קיימת פרבולה שנקודות החיתוך שלה עם ציר ה- x שונות מנקודות החיתוך של פונקציות הקוויות?