הקדמה: 

המפה הטופוגראפית נועדה לתת מידע לגבי צורתו החיצונית של השטח, באופן הקרוב ביותר למציאות. במפה הטופוגראפית יש מידע על תבליט השטח המיוצג באמצעות קווי גובה.

קווי גובה הם קווים דמיוניים מהם ניתן ללמוד את הצורה של פני השטח.

כל נקודה על אותו קו גובה נמצאת באותו הגובה מעל פני הים. הפרשי הגובה בין שני קווי גובה סמוכים במפה הוא קבוע.

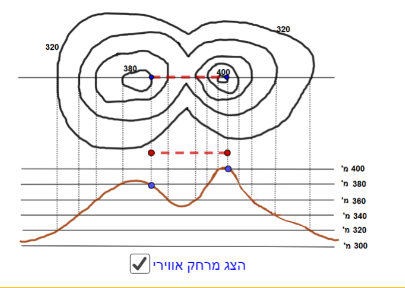
למשל בדוגמה בצד שמאל ההפרש הקבוע בין שני קווי גובה סמוכים הוא 20 מ'.

במפה הטופוגרפית על חלק מקווי הגובה מצויין הגובה, ובין שני קווי גובה כאלה יש תמיד קווי גובה שעליהם לא מצויין הגובה.

למשל בדוגמה בצד שמאל מצויין קו הגובה 320 מ' וקו הגובה 400 מ', אך קוי הגובה שביניהם (340 מ', 360 מ', 380 מ') לא ממוספרים.

המפה הטופוגראפית, כמו כל מפה רגילה, ערוכה בקנה מידה.

מרחק אווירי בין שתי נקודות במפה הוא הקטע הישר הנמדד בין שתי נקודות במפה. חישוב אורך הקטע הזה במציאות לפי קנה המידה של המפה לא לוקח בחשבון את הפרשי הגובה בין שתי הנקודות. הוא למעשה מודד את המרחק בין שתי הנקודות כפי שהוא נראה ממעוף ציפור שעפה בין שתי הנקודות מבלי לשנות את גובה מעופה.

למשל בדוגמה בצד שמאל, המרחק האווירי בין שתי הנקודות הכחולות במפה מסומן בקו אדום מקוקו (להצגתו לחצו בתיבה).

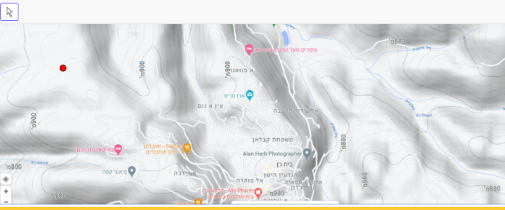
במשימה 1, התלמיד מתבקש לסמן במפה 3 דוגמאות שונות של מקומות שגובהם מעל פני הים הוא  900 מטרים (באמצעות הזזת הנקודה האדומה). 

המטרה של משימה זו היא לבדוק אם התלמיד מבין שכל נקודה על קו גובה המסומן ב- 900 מ' נמצאת בגובה 900 מ' מעל פני הים.

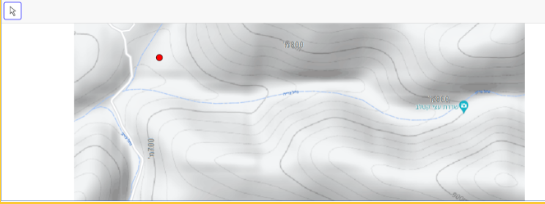
במשימה 2, התלמיד מתבקש לסמן במפה 3 דוגמאות שונות של מקומות שגובהם מעל פני הים הוא  760 מטרים (באמצעות הזזת הנקודה האדומה). 

המטרה של משימה זו היא לבדוק אם התלמיד מבין שהפרשי הגובה בין שני קווי גובה סמוכים במפה הוא קבוע. 

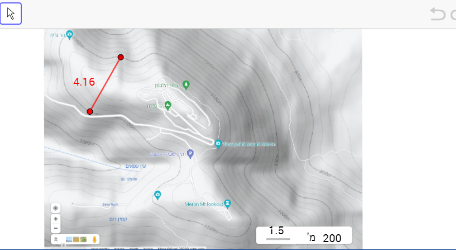
במשימה 3, נתון כי באתר הר מירון החליטו להקים שני חניוני לילה בגובה 1100 מטרים מעל פני הים, ונתונות  3 הצעות למרחק האווירי בין שני החניונים.

התלמיד מתבקש לבחור את ההצעות שיכולות להתקיים, ולכל הצעה כזאת להגיש דוגמה תומכת למיקום החניונים על ידי גרירת הנקודות האדומות בסרטוט למקום מתאים (שתי הנקודות האדומות מייצגות את החניונים).

שימו לב – כל קטע באורך 1.5 יחידות במפה הוא 200 מ' במציאות.

הצעה א : שני החניונים הם במרחק אווירי של 1.8 ק"מ זה מזה

הצעה ב: שני החניונים הם במרחק אווירי של 2.4 ק"מ זה מזה

הצעה ג: שני החניונים הם במרחק אווירי של 640 מטרים זה מזה

המטרה של משימה זו היא לבדוק אם התלמיד יודע להשתמש בקנה המידה הנתון תוך שימוש בהמרת יחידות. 

במשימה 4, נתון כי חברת חשמל הקימה מערך של עמודי חשמל שווים בגובהם בסביבת הר מירון. העמודים ממוספרים מעמוד 1 עד 13 . בין כל שני עמודים סמוכים נמתח באותו הגובה כבל חשמלי.

במפה הטופוגרפית מסומנים עמודי החשמל באמצעות נקודות כחולות. 

המרחק הקווי האווירי בין כל שני עמודים סמוכים הוא גודל קבוע.

כמו כן, נתונות שתי טענות. התלמיד מתבקש להגיש לכל טענה דוגמה תומכת על ידי סימון שני זוגות של עמודי חשמל מתאימים (שימו לב – על מנת לסמן זוג חדש של עמודי חשמל צריך לבטל את הסימון של אחת התיבות שנבחרו קודם) .

1. קיימים שני כבלים חשמליים שווים באורכם שעוברים בין שני עמודי חשמל סמוכים
2. קיימים שני כבלים חשמליים שונים באורכם שעוברים בין שני עמודי חשמל סמוכים

המטרה של משימה זו היא לבדוק אם התלמיד מבין שהפרש הגובה בין שני העמודים הוא המשפיע, כי המרחק האווירי קבוע. כלומר, שני כבלים חשמליים שווים באורכם זה אומר שיש אותו הפרש גובה בין שני העמודים,  ושני כבלים חשמליים שונים באורכם זה אומר שהפרש הגובה בין שני העמודים הוא שונה. 

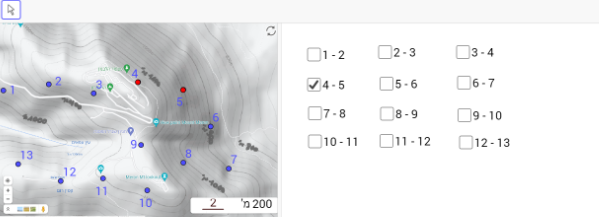
במשימה 5, נתון כי חברת החשמל הקימה מערך של עמודי חשמל שווים בגובהם בסביבת הר מירון. בין כל שני עמודים סמוכים נמתח באותו הגובה כבל חשמלי.

במפה הטופוגרפית מסומנים עמודי החשמל באמצעות נקודות כחולות הממוספרות מ- 1 עד 13 .

המרחק האווירי בין כל שני עמודים סמוכים הוא 4.5 יחידות במפה.

כמו כן, נתונות טענות. התלמיד מתבקש לבחור את הטענות הנכונות, ולכל טענה נכונה להגיש דוגמה תומכת ע"י סימון שני עמודי חשמל מתאימים.

1. קיימים שני עמודי חשמל שאורך הכבל המתוח ביניהם הוא גדול מ- 460 מ'
2. קיימים שני עמודי חשמל שאורך הכבל המתוח ביניהם הוא בדיוק 450 מ'
3. קיימים שני עמודי חשמלי שאורך הכבל המתוח ביניהם הוא קטן מ- 450 מ'

המטרה של משימה זו היא לבדוק אם התלמיד יודע להשתמש במשפט פיתגורס כדי לחשב את אורך הכבל החשמלי, כשידוע לו שהמרחק האווירי בין כל שני עמודים סמוכים הוא 4.5 יחידות במפה.

שימו לב כי בשונה ממשימה 4 שאפשר לפתור רק דרך חפיפת משולשים, במשימה 5 התלמיד חייב לחשב לפי משפט פיתגורס תוך שימוש בחישובי קנה מידה. 

הפעילות עוסקת במפה טופוגראפית, שכמו כל מפה רגילה ערוכה בקנה מידה שהוא היחס בין גודל בשרטוט לבין גודל במציאות.

נושא "קנה מידה" נלמד בכיתה ח', כך שלפי תוכנית הלימודים "יש למצוא קנה מידה על פי מידות נתונות בשרטוט ובמציאות, יש למצוא גודל במציאות על פי קנה המידה והגודל שנמדד בשרטוט, ויש למצוא גודל בשרטוט על פי קנה המידה והגודל הנתון שבמציאות."

העיסוק בקנה מידה כולל חישובים והמרות של יחידות אורך שונות. 

(ראה עמוד 62 בתוכנית הלימודים של חט"ב) 

משימה 4 בפעילות הזו עוסקת בנושא "חפיפת משולשים" (בפרט חפיפה על פי צלע-זווית-צלע) שגם הוא נלמד בכיתה ח'.    

לפי תוכנית הלימודים, המטרה מלימוד נושא זה היא "להכיר את שלושת משפטי החפיפה הראשונים, להצדיק את נכונותם וללמוד להסיק שוויון של צלעות וזוויות מתוך ידיעה ששני משולשים הם חופפים, כך שנכונות משפטי החפיפה תודגם באמצעים קדם-דדוקטיביים, וללא הוכחות פורמליות." 

(ראה עמוד 65 בתוכנית הלימודים של חט"ב) 

משימה 5 בפעילות הזו עוסקת בנושא "משפט פיתגורס" שנלמד בכיתה ט'. 

לפי תוכנית הלימודים "השימוש במשפט פיתגורס מצריך חישוב שורש ריבועי, ולימוד זה משתלב עם העיסוק בשורשים בתחום המספרי", כמו כן, "מומלץ לעסוק בבניות שבהן יש להסיק נתונים חסרים בעזרת משפט פיתגורס, ובנוסף יש לעסוק בבעיות המשלבות בין משפט פיתגורס לבין עובדות שנלמדו בכיתות ז-ח." 

(ראה עמוד 95 בתוכנית הלימודים של חט"ב) 

לכן, ניתן להעביר את שלושת המשימות הראשונות של הפעילות בכיתה ח' כמשימות תרגול בנושא קנה מידה. 

כמו כן, ניתן להעביר את הפעילות כולה כפעילות מסכמת בכיתה ט' לתלמידים אשר למדו את משפט חפיפת משולשים צ.ז.צ ומשפט פיתגורס.

קנה מידה (למשימה 3 עד 5)

חפיפת משולשים על פי צלע-זווית-צלע (למשימה 4)

משפט פיתגורס (למשימה 5) 

משימה 1:

כל נקודה שהיא על קו גובה 900 מ'.

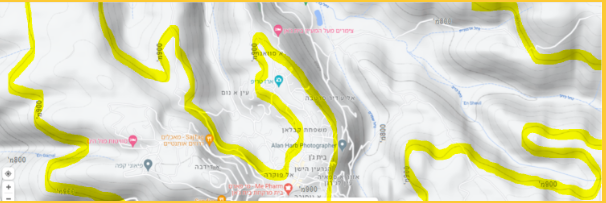
משימה 2: 

כל נקודה שהיא על קו הגובה השלישי בין קוי הגובה 700 מ' ו- 800 מ'. 

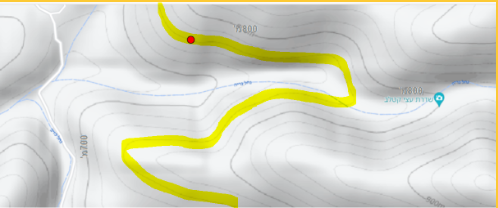
משימה 3:

יש לשים לב כי קודם צריך להמיר מק"מ למ', ולאחר מכן להשתמש בקנה המידה הנתון שכל קטע באורך 1.5 יחידות במפה הוא 200 מ' במציאות.

הצעה א : שני החניונים הם במרחק אווירי של 1.8 ק"מ זה מזה, כלומר :  1.8×1000:200×1.5=13.5  לכן צריך לחפש קטע באורך 13.5 במפה. למשל: 

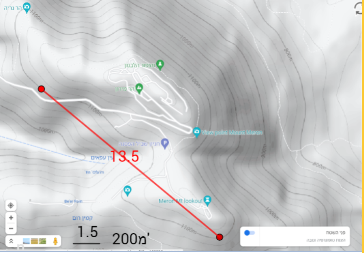
הצעה ב: שני החניונים הם במרחק אווירי של 2.4 ק"מ זה מזה, כלומר: 2.4×1000:200×1.5=18  לכן צריך לחפש קטע באורך 18 במפה. 

אין קטע באורך זה כי הקטע הכי ארוך הוא באורך 17.8

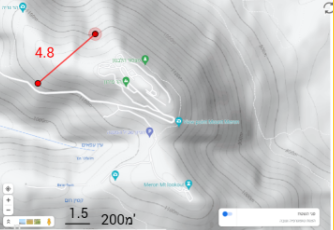
הצעה ג: שני החניונים הם במרחק אווירי של 640  מטרים זה מזה, כלומר: 640:200×1.5=4.8  לכן צריך לחפש קטע באורך 4.8 במפה. למשל: 

משימה 4:

שני כבלים חשמליים שווים באורכם זה אומר שיש אותו הפרש גובה בין שני העמודים. דוגמאות התומכות בטענה 1 :

1. העמודים 2 ו-3   והעמודים 10 ו- 11 , ההפרש בין כל שני עמודים סמוכים הוא 20 מ' וידוע כי המרחק האווירי קבוע, לכן המשולשים יהיו חופפים. 

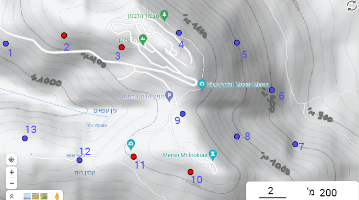
2. העמודים 10 ו-9 , 12 ו-13 , כל זוג עמודים נמצא על אותו גובה וגם ידוע כי המרחק האווירי קבוע, לכן המשולשים הנוצרים בין כל זוג יהיו חופפים.

3. העמודים 8 ו- 9 , 1 ו- 2 , ההפרש בין כל שני עמודים סמוכים הוא 100 מ' וידוע כי המרחק האווירי קבוע, לכן המשולשים יהיו חופפים.

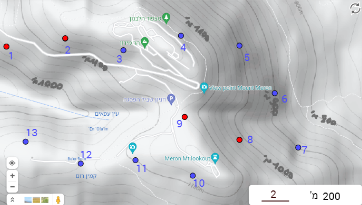
שני כבלים חשמליים שונים באורכם זה אומר שהפרש הגובה בין שני העמודים הוא שונה.

דוגמאות התומכות בטענה 2:

1. ההפרש בין העמודים 1 ו- 2 הוא  100 מ' , ההפרש בין  4 ו- 5 הוא 160 מ' וידוע כי המרחק האווירי קבוע, לכן המשולשים לא יהיו חופפים. 

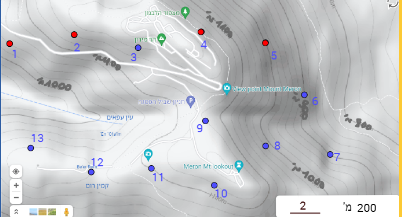
2. ההפרש בין העמודים 6 ו- 7 הוא  0 מ' (על אותו גובה), ההפרש בין  7 ו- 8 הוא 120 מ' וידוע כי המרחק האווירי קבוע, לכן המשולשים לא יהיו חופפים.

משימה 5:

טענה 1 – נכונה:

קיימים שני עמודי חשמל שאורך הכבל המתוח ביניהם הוא גדול מ- 460 מ', למשל:

עמודים 7 ו-8 

ההפרש בין העמודים הוא 120 מ', ונתון שהמרחק האווירי ביניהם הוא 4.5 יחידות במפה כלומר לפי חישוב קנה מידה הוא 450 מ'. לכן, לפי פיתגורס נקבל שאורך הכבל (המיתר במשולש ישר זווית) הוא 465.7 מ' 

פתרון אלגברי:

טענה 2 – נכונה: 

קיימים שני עמודי חשמל שאורך הכבל המתוח ביניהם הוא בדיוק 450 מ', למשל:

שני העמודים 3 ו- 4 על אותו גובה (כלומר ההפרש 0), ונתון שהמרחק האווירי ביניהם הוא 450 מ' (אחרי חישוב קנה מידה). לכן, נקבל שאורך הכבל הוא 450 מ'.

טענה 3 – לא נכונה: 

לא קיימים שני עמודי חשמלי שאורך הכבל המתוח ביניהם הוא קטן מ- 450 מ', כי כבל באורך 450 מ' הוא בין שני עמודים על אותו גובה. 

חשוב לעבור על ההקדמה וההסבר על מפה טופוגרפית לפני פתרון המשימות. 

משימה 1: 

• בדיון עם התלמידים יש להתייחס לעקום בצד ימין למעלה (שלא כתוב עליו הגובה). 
• יש לוודא שהתלמידים מבינים שכל הנקודות על קו גובה מסויים מסמלות מקומות באותו גובה במציאות.

משימה 2: 

• יש להדגיש לתלמידים שבין כל שני קווי גובה מודגשים, יש 4 קווי גובה שההפרש ביניהם הוא קבוע.

• יש לדון עם התלמידים באופן חישוב הפרשי הגובה בין שני קווי גובה סמוכים במפה. למשל אם בין קו גובה 700 מ' וקו גובה 800 מ' יש 4 קווי גובה, זה אומר שכל אחד מהם נמצא בהפרש 20 מ' (במקרה הזה קווי הגובה הם: 720 מ', 740 מ', 760 מ', 780 מ')

משימה 3:

• יש לדון עם התלמידים באופן חישוב המרחק האווירי לפי קנה המידה הנתון ואופן המרת היחידות מ-ק"מ ל- מ'.  

משימה 4:

• יש לוודא שהתלמידים מבינים שהפרש הגובה בין שני העמודים הוא המשפיע על אורך הכבל החשמלי, כי המרחק האווירי קבוע. כלומר, שני כבלים חשמליים שווים באורכם זה אומר שיש אותו הפרש גובה בין שני העמודים,  ושני כבלים חשמליים שונים באורכם זה אומר שהפרש הגובה בין שני העמודים הוא שונה. 
• יש להזכיר לתלמידים את משפט חפיפת המשולשים לפי צ.ז.צ.

משימה 5: 

• יש לוודא שהתלמידים מבינים שאורך הקו האווירי בין שני העמודים במציאות הוא 450 מ' (לפי חישובי קנה מידה   4.5×200:2 = 450 ).
• חשוב להזכיר לתלמידים את משפט פיתגורס ואופן הצבת המספרים הנתונים בו. 

• יש לוודא שהתלמידים מבינים ש:

אם שני עמודים על אותו גובה אז ההפרש הוא 0, ולכן אורך הכבל הוא שווה לאורך הקו האווירי שהוא 450 מ'. 

אם שני עמודים נמצאים בגבהים שונים אז אורך הכבל יהיה גדול מ 450 מ'. 

אין כבל שאורכו קטן מ- 450 מ'.