מטרת הפעילות לתת לתלמידים אבני הבנייה להוכחת משפט חוצה זווית פנימית במשולש.הוכחת המשפט מבוססת על שטחי משולשים.

הפעילות מתאימה לתלמידי כיתות ט וכיתות י. בתוכנית הלימודים של מתמטיקה ניתן דגש מיוחד לשטחים ולשטח משולש בפרט ולכן הוכחות בגיאומטריה המבוססות על שטחים נושא שחשוב לשלב בהוראה בכיתה.

• הגדרה של חוצה זווית פנימית במשולש
• חוצה זווית כמקום גיאומטרי של מרחקים משוקי הזווית
• משולשים שווי שטח.
• יחס בין שטחי משולשים בעלי גובה משותף

אפשר לחלק את הפעילות לשני חלקים. בחלק הראשון 3 משימות: משימה 1_1, משימה 2_1 ומשימה 3_1.

תיאור המשימה

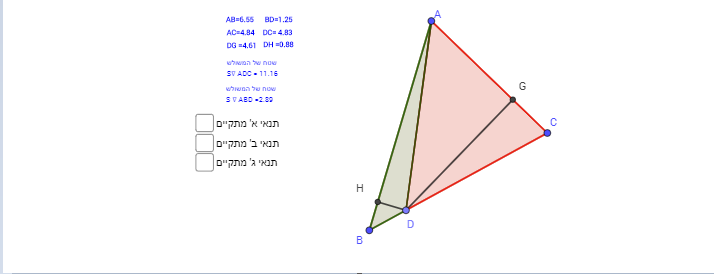
בסרטוט הדינאמי נתון משולש ABC ונתונים תנאים 

מנקודה D הנמצאת על הצלע BC בונים שני אנכים DG ו- DH לצלעות AC ו AB בהתאמה.

טענה: קיים משולש ABC שבו בדיוק תנאי אחד מהתנאים הנתונים מתקיימים.

האם הטענה נכונה? כן/לא

לחיצה על תיבות הבחירה "נועלות" את השרטוט לפי התנאי. לדוגמה, לחיצה על תנאי DH=DG משרטטת משולשים בהם DH=DG 

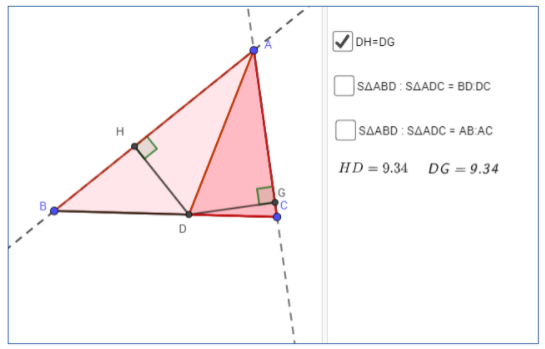
במשימה, תלמידים מתבקשים לסמן תנאי אחד בלבד, זאת אומרת תנאי אחד שאף תנאי אחר אינו שקול לו. התנאי היחיד שמתאים לטענה הוא :

S∆ABD:S∆ADC = BD:DC

התנאי הזה מתקיים בכל המשולשים תמיד, כי לשני משולשים אותו גובה היוצא מקודקוד A.

משימה 2_1 תיאור המשימה:

בסרטוט הדינאמי נתון משולש ABC ונתונים תנאים 

מנקודה D הנמצאת על הצלע BC בונים שני אנכים DG ו- DH לצלעות AC ו AB בהתאמה.

טענה: קיים משולש ABC שבו בדיוק שני תנאים מהתנאים הנתונים מתקיימים.

האם הטענה נכונה? כן/לא

טבלת תשובות אפשריות:

תנאים ביישומון:

1. DH=DG
2. S∆ABD:S∆ADC = BD:DC
3. S∆ABD:S∆ADC = AB:AC

משימה 3_1

בסרטוט הדינאמי נתון משולש ABC ונתונים תנאים 

מנקודה D הנמצאת על הצלע BC בונים שני אנכים DG ו- DH לצלעות AC ו AB בהתאמה.

טענה: קיים משולש ABC שבו שלושת התנאים הנתונים מתקיימים.

האם הטענה נכונה? כן/לא

התשובה במשימה הזאת היא כן, קיים משולש כזה.

*המלצה:  בשלב הזה של השיעור כדאי לעשות דיון בכיתה. בנוסף לנכונות ההגשות, אפשר לבדוק אלה סוגי משולשים תלמידים הגישו.הפילטרים שבנינו מזהים משולשים שווי שוקיים ומשולשים שווי צלעות בהגשות של תלמידים.

 הוכחת משפט:

חוצה זווית פנימית במשולש מחלק את הצלע שמול הזווית לשני קטעים אשר היחס ביניהם שווה  ליחס הצלעות הכולאות את הזווית בהתאמה.

S∆ABD:S∆ADC = BD:DC טענה זו מתקיימת בכל משולש כי לשני המשולשים יש אותו גובה (גובה משותף)

S∆ABD:S∆ADC = AB:AC טענה זו מתקיים כאשר AD חוצה זווית בלבד לפי הגדרת חוצה זווית כמקום גיאומטרי של מרחקים משוקיי הזווית.

       ⇓

BD:DC = AB:AC

צ'ביאן – משימות 2, צ'ביאן – משימות 3

צ'ביאן הוא קטע במשולש המחבר קודקוד עם הצלע שמולו. משימות אלה עוסקות בתכונות של צ'ביאנים שונים.

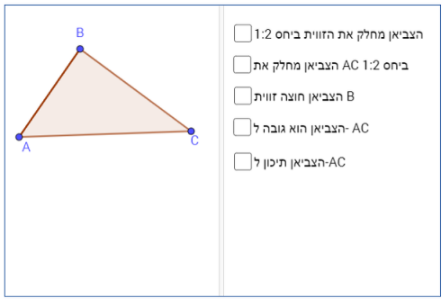
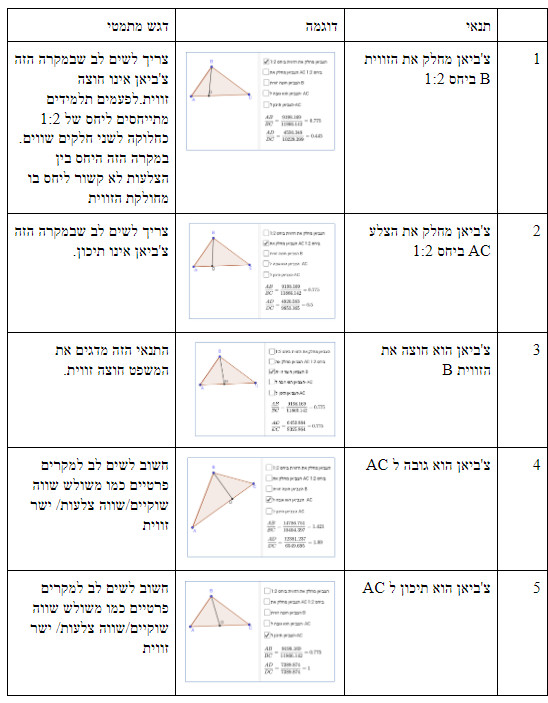
מקרים של שניים ושלושה תנאים:

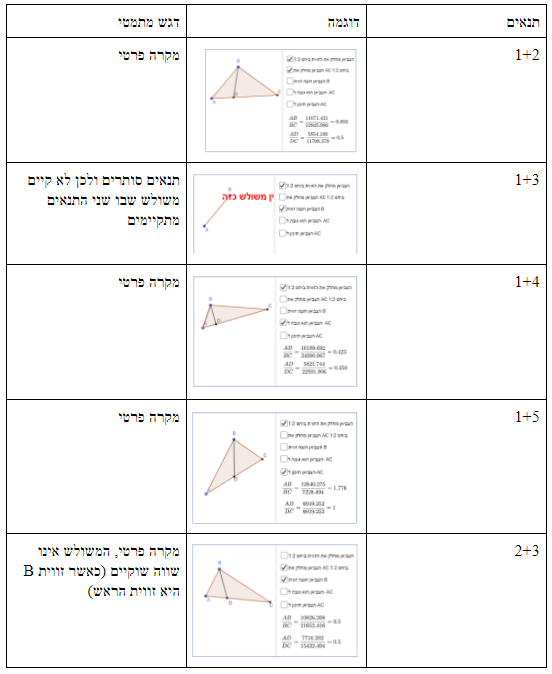
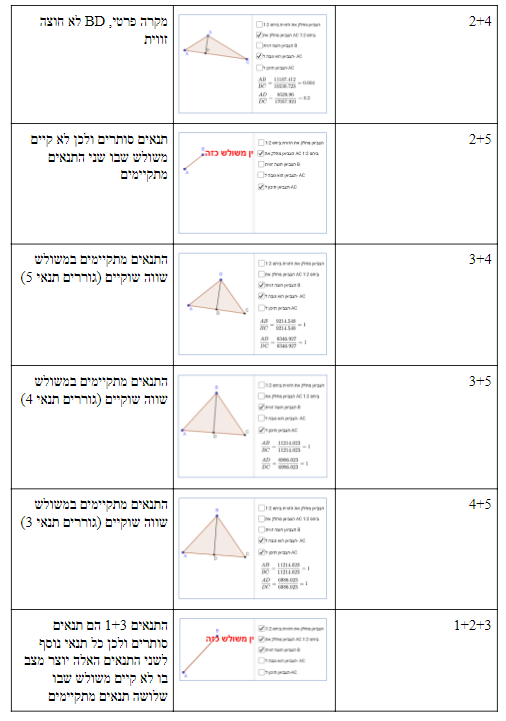
משימה 1 – לא קיימים פילטרים – מומלץ לשלב את הפילטרים הבאים:

• משולש שווה שוקיים.
• משולש כהה זווית.
• ישר זווית.
• חד זווית.
• שווה צלעות.
• הגבהים מהנקודה D לצלע AC ולצלע AB שווים באורכם.
• יחס השטחים SΔABD : SΔADC שווה ליחס הצלעות BD:DC​.
• יחס השטחים :  SΔABD : SΔADCשווה ליחס הצלעות: AB:AC.

משימה 2 – הפילטרים קיימים

• משולש שווה צלעות.
• הקטע הוא גובה ל-AC והיחס שווה.
• הקטע הוא ח"ז B והיחס שווה.
• הקטע הוא תיכון לצלע AC והיחס שווה.
• הקטע מחלק את הצלע ביחס של 1:2 והיחס שווה.
  
  משימה 3 – הפילטרים קיימים
• משולש שווה צלעות.
• הקטע הוא גובה ל-AC והיחס שווה.
• הקטע הוא ח"ז B והיחס שווה.
• הקטע הוא תיכון לצלע AC והיחס שווה.
• הקטע מחלק את הצלע ביחס של 1:2 והיחס שווה.

אפשר לבדוק עם התלמידים באילו משולשים מתקיים תנאים ובאילו משולשים לא מתקיימים התנאים ולבקש להוכיח את הטענות.