פונקציית מנה של שורש
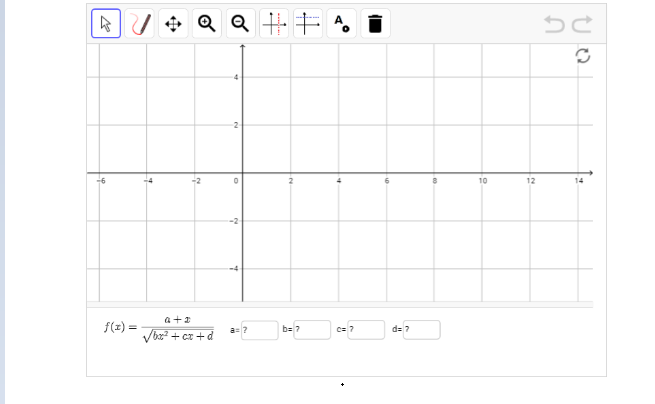
בניית פונקציית מנה עם שורש על סמך הנתונים, התייחסות לתחום ההגדרה, נקודות חיתוך עם צירים, אסימפטוטות מקבילות לצירים, תחומי עליה וירידה, זוגיות ואי-זוגיות של הפונקציה.
קישור לכיתת התנסות
הקניית ידע על משפחת פרמטרים של פונקציה, מציאת ערך הפרמטר באמצעות נתונים שונים, חקירה על סמך נתונים בדרך עקיפה ובניית פונקציה, סיכום פרק חקירת פונקציה, למידה מטעויות של העמיתים.
פעילות מתאימה לכיתות י"א אכן לומדים 5 יח"ל מתמטיקה, ניתן להעביר את הפעילות אחרי שהתלמיד למד פרק חקירת פונקציות מכל הסוגים (פונקציית פולינום, מנה ושורש),ותרגל על שאלות חקירה עם פרמטרים, ובמיוחד עם אסימפטוטות (ידע נדרש), מכיוון שאנו נתקלים עם התלמידים בסוגית הפחד לשאלות עם פרמטרים, גם כן חלק לא מעט מהתלמידים ייקח להם זמן להבין מה משמעות הפרמטר, ואך למצוא ערכו בשאלה. עם זה ברוב שאלות הבגרות יש לכל היותר שני פרמטרים בשאלה, ובפעילות הזו יש בה ארבעה פרמטרים וזה לא קל לתלמיד.
לכן מומלץ למורה לתכנן שיעור כפול 90דק' בכיתת מחשבים, בתקופה בה התלמידים תרגלו ופתרו שאלות חקירה מליאה . יבחר המורה לשיעור שאלת בגרות לפתיחה, שאלה של פונקציית מנה עם שורש, כוללת שני פרמטרים ואחד מסעיפיה צריך להוכיח אם הפונקציה זוגית או אי זוגית. במהלך פתירת השאלה ביחד, המורה עוד פעם יסביר את משמעות הפרמטרים בשאלה ויתייחס לעוד מקרים אשר יש משמעות אחרת לפרמטר. ובסוף המורה יציג מול התלמידים את הפעילות, ייתן להם את היוזרים אכן כל תלמיד והיוזר שלו מודפס על תלוש נייר, יסביר המורה מה צריך לעשות. ייתן להם רבע שעה עד 20דק' לפתירת המשימה ולהסתובב בניהם ובלי עזרה לאף תלמיד.
פילטרים (טענה נכונה\ לא נכונה), מציג אם התלמיד הבין את השאלה או לא, כי בתשובות של התלמידים חלק מהם סימן בטענה נכונה והם רק בוחרים בשלושה תנאים, אזי כמובן הם לא הבינו מה מבוקש מהם, אכן צריכים למצוא פרמטרים עבורם את כל החמישה התנאים נכונים.
פילטר הבחירה בתנאי, זה כן פילטר מציג את הבנת התלמיד לתנאי אם מתקיים התנאי בהגשה שלו ואם הוא לא בחר בו, או ההפך.
פילטרים לתנאים עצמם אם קיימים או לא, אלה הפילטרים הכי חשובים ולפיהם אנו פותחים דיון בכיתה.
פילטר הוגש הסבר, נוכל להבין אם התלמיד חשב לעומק על המשימה או לא, אם הוא מבין למה או בחר בתנאים.
הצעת פילטרים חדשים:
פילטר להצגת ערך הפרמטר, זה נותן יותר למורה להבין אם התלמיד פתר את השאלה מתוך ניסוי וטעייה או מתוך חשיבה על ערכים לפרמטרים נכונים.
מכיוון שכל התלמידים שהוגשו את המשימה ידעו ויכלו למצוא את הערכים שעבורם תחום ההגדרה הנתון הוא נכון, כמובן הערכים הן לפרמטרים b,d,c. לכן לפי זה יבוקש מאחד התלמידים להציג את פתרונו, ונציג את כל התשובות שתחום ההגדרה שלהם נכון, ומזה ננסה להבין איך מתנהגת הפונקציה אם תחום הגדרה הוא x>4 או x<2 .בתשובות יש אחד אשר בוחר בתחום ההגדרה x>4 או x<2 אך הציור מראה שהפונקציה מוגדרת לכל X גם לזה נתייחס, אבל לדעתי שהתלמיד כאן התבלבל בהגשת המשימה. גם כן יש הגשה הוא בוחר בתחום הזה והציור מראה שהתחום הוא x>-2 או x<-4 , מהתשובה הזו ננסה להבין למה התלמיד בחר בתחום ההגדרה הנתון אך התשובה מלאה אחרת, אזי בשלב הזה ילמדו מטעויות וינסו להבין את הטעות או מאיפה באה.
לגבי האסימפטוטות כמובן שאחד מהתלמידים יגיב שהאסימפטוטות האנכיות הנכונות הן x=2 , x=4
ובכך קיבלנו עוד תנאי נכון, שוב נציג את כל התשובות אשר הם נכונות וננסה מהם להגיע לתשובה הנכונה לגבי האסימפטוטות האופקיות.
אחרי זה ניתן לתלמידים שתי דקות כדי למצוא את נקודות החיתוך עם הצירים באמצעות a, ונחזור לתנאים של המשימה וכמובן יקבלו שערך a שווה ל -3, ומהתשובות נקבל שרק שניים מהם יש להם תשובות נכונות,ואז כל אחד ייקח לו שתי דקות להבין מה הוא עשה כאשר הגיש את המשימה על מה חשב למה לא הקיבל שהתנאי נכון? ויעלו את הטעויות שלהם בפני כל הכיתה ובכך ילמד אחד מהשני על מה אנחנו לפעמים חושבים ולמה אינם נכונים.







