הקדמה לכל המשימות:

עמית ומורן החליטו להתאמן ביחד לקראת מרוץ האופניים בתחרות איש הברזל. אורך המסלול בתחרות איש הברזל הוא 180 ק"מ.

שתי החברות החליטו לקבוע לפני כל אימון את המסלול שבו ייערך האימון. לעיתים הן יצאו לרכיבה מאותו קצה של המסלול הנבחר ולעיתים מקצוות שונים של המסלול שנבחר.

בכל מקרה כל אחת מהרוכבות רכבה עד הקצה האחר של המסלול. 

עמית יצאה לכל אימון בשעה 8:00 בבוקר. מורן לא התחייבה לצאת בשעה מסוימת  אבל היא התחייבה בכל אימון לחלוף על פני עמית במקום כלשהו לאורך המסלול כדי להעלות את המוטיבציה של שתיהן וליצור אווירה של שיתופיות באימון.

נניח שכל אחת מהרוכבות רוכבת במהירות אחידה לכל אורך הדרך והמהירות שבה ניתן לרכוב על אופניים נעה בין 6 קמ"ש ל- 40 קמ"ש.

ביישומון של משימות 1-3 מופיעים גרפים המתארים את מיקומן של שתי הרוכבות יחסית לנקודת ההתחלה של עמית בשעה 8 בבוקר.

בחלון השמאלי ביישומון, הגרף הכחול מתאר את המיקום של עמית כך שניתן להזיז את הנקודה הכחולה כדי לשנות את זמן ההגעה שלה. הגרף הכתום מתאר את המיקום של מורן כך שניתן להזיז את הנקודה הכתומה כדי לשנות את זמן היציאה שלה. 

כמו כן, ניתן להזיז את הנקודה החומה על ציר Y כדי לשנות את אורך המסלול בק"מ.

התלמידים יכולים להיעזר בקווי העזר הנתונים ובישרים המקבילים לצירים.

ע"י הפעלת ההדמיה, מתקבלת נקודה אדומה המתארת את המיקום של עמית לפי המסלול שלה, ונקודה ירוקה המתארת את המיקום של מורן לפי המסלול שלה.

המטרה הכללית של הפעילות היא להשתמש בדמיון משולשים כדי לפתור בעיית תנועה, בלי שימוש בביטויים אלגבריים.

במשימה 1 נתונים תיאורים. התלמיד מתבקש להגיש לכל תיאור גרף מתאים.

התיאורים:

1. מורן ועמית בחרו מסלול שאורכו 60 ק"מ. שתיהן יצאו לרכיבה . מורן יצאה לדרך אחרי השעה .8:00 בבוקר. עמית פגשה את מורן במחצית הזמן שלקח לעמית להשלים את כל המסלול.
2. מורן ועמית בחרו מסלול שאורכו 100 ק"מ. עמית יצאה לרכיבה מקצה אחד של המסלול מורן מהקצה השני שלו. מורן יצאה לדרך לפני עמית והגיע לקצה המסלול באותה השעה שעמית הגיעה לקצה המסלול שלה.
3. מורן ועמית יצאו לרכיבה מאותו המקום במסלול שקבעו.. עמית פגשה את מורן בשעה 11:00. מורן רכבה יותר מ- 3 שעות עד שחלפה ליד עמית

במשימה 2 נתונים שני תיאורים:

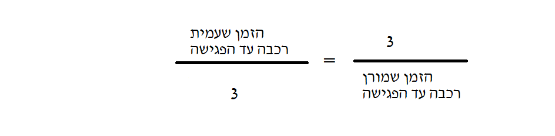
תיאור 1: היחס בין הזמן שעמית רכבה ממקום יציאתה עד הפגישה לבין זמן הרכיבה שלה אחרי הפגישה עד שהגיע לסוף המסלול הוא 1:2

תיאור 2: היחס בין הזמן שמורן רכבה ממקום יציאתה עד הפגישה לבין זמן הרכיבה שלה אחרי הפגישה עד שהגיע לסוף המסלול הוא 1:2

כמו כן, נתונות שתי טענות.

התלמיד מתבקש לסמן את הטענה הנכונה מביניהן ולהגיש גרף מתאים התומך בטענה.

התלמיד מתבקש להגיש גרף מתאים לכל טענה.

1. שני התיאורים יכולים להתקיים באותו אימון
2. רק אחד מהתיאורים יכול להתקיים באותו אמון

במשימה 3 נתון כי מורן ועמית יצאו לרכיבה מקצוות שונים של המסלול.

היחס בין הזמן שעמית רכבה ממקום יציאתה עד הפגישה לבין זמן הרכיבה שלה מהפגישה עד שהגיעה לסוף המסלול שווה ליחס בין הזמן שמורן רכבה ממקום יציאתה עד הפגישה, לבין זמן הרכיבה של מורן מהפגישה עד שהגיע לסוף המסלול. 

התלמיד מתבקש להגיש 3 דוגמאות שונות של גרפים שמתאימים לתיאור

ביישומון של משימות 4-6 מופיעים גרפים המתארים את מיקומן של שתי הרוכבות יחסית לנקודת ההתחלה של עמית בשעה 8 בבוקר.

בחלון השמאלי ביישומון, הגרף הכחול מתאר את המיקום של עמית והגרף הכתום מתאר את המיקום של מורן. ניתן להזיז את הנקודה החומה על ציר Y כדי לשנות את אורך המסלול בק"מ. כמו כן, התלמידים יכולים להיעזר בקווי העזר הנתונים.

ע"י הפעלת ההדמיה, מתקבלת נקודה אדומה המתארת את המיקום של עמית לפי המסלול שלה, ונקודה ירוקה המתארת את המיקום של מורן לפי המסלול שלה.

במשימה 4 נתון כי מורן ועמית יצאו לרכיבה מאותו המקום.

מורן רצתה לפגוש את עמית בדרך 4 שעות אחרי שמורן יצאה לרכיבה.

כמו כן, נתונות שתי טענות.

התלמיד מתבקש להגיש דוגמה תומכת לכל טענה.

1. מורן יצאה לרכיבה אחרי עמית
2. מורן יצאה לרכיבה לפני עמית

במשימה 5 נתון כי מורן ועמית יצאו לרכיבה מקצוות שונים של אותו המסלול.

מורן רצתה להגיע לקצה המסלול 4 שעות אחרי שתחלוף על פני עמית.

כמו כן, נתונות טענות.

התלמיד מתבקש להגיש לכל טענה דוגמה תומכת.

1. כדי למלא את רצונה מורן יכולה לצאת לרכיבה באותה השעה שעמית יצאה לרכיבה.
2. כדי למלא את רצונה מורן יכולה לצאת לרכיבה אחרי עמית
3. כדי למלא את רצונה מורן יכולה לצאת לרכיבה לפני עמית

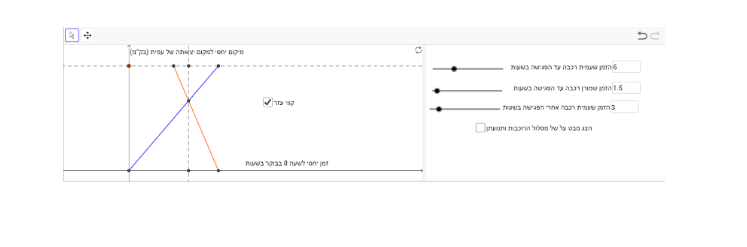
במשימה 6  נתון כי מורן ועמית יצאו לרכיבה מקצוות שונים של המסלול .

מורן ועמית רצו להגיע כל אחת לקצה המסלול 3 שעות לאחר שחלפו זו פני זו.

כמה זמן צריכה כל אחת מהן לרכב עד לנקודת המפגש? 

התלמיד מתבקש להגיש 3 דוגמאות שונות ככל האפשר.

נושא "דמיון משולשים" נלמד בכיתה ח' , כך שלפי תוכנית הלימודים "יש ללמוד למצוא נתונים חסרים מתוך תכונת הדמיון ותוך שימוש בפרופורציה….כמו כן, יש לעסוק בבעיות המשלבות בין דמיון משולשים ובין עובדות שנלמדו בכיתה ז' ובתחילת כיתה ח' , תוך שילוב דוגמאות מחיי היומיום" (ראה עמוד  88   בתוכנית הלימודים של חט"ב).

כמו כן, נושא ייצוג תופעות באמצעות פונקציות קוויות נלמד בכיתה ח' כך שלפי תוכנית הלימודים "יש לעסוק בפונקציות קוויות בהקשר של שאלות מילוליות ויש לפתור בעיות המתארות תהליכי השתנות באמצעות פונקציות קוויות". (ראה עמוד  55   בתוכנית הלימודים של חט"ב).

לכן ניתן להעביר פעילות זו בהקשר של בעיות תנועה בשילוב עם דמיון משולשים, כפעילות תרגול או סיכום עבור תלמידים אשר למדו שני נושאים אלה.

הבנת הקשר בין מרחק, זמן, מהירות

קריאת גרפים 

דמיון משולשים ויחס בין כל שתי צלעות (משפט תאלס) 

משימה 1

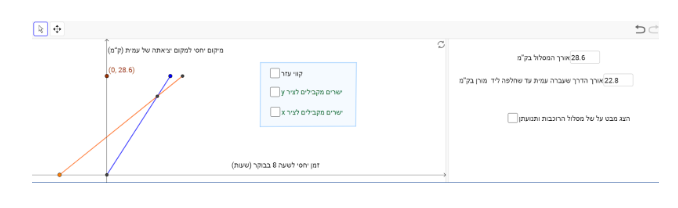
תיאור 1: עמית פגשה את מורן במחצית הזמן שלקח לעמית להשלים את כל המסלול כלומר אחרי 30 ק"מ .

לא נתון מאיזה קצה מורן יצאה, לכן ישנן כמה אפשרויות. למשל:

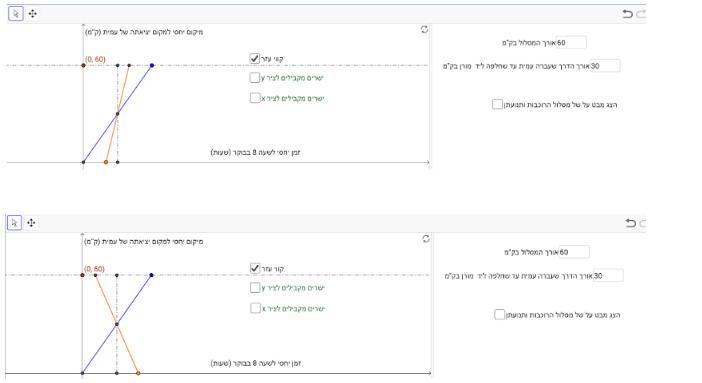
 תיאור 2: עמית יצאה לרכיבה מקצה אחד של המסלול ומורן מהקצה השני שלו. מורן יצאה לדרך לפני עמית. לכן הנקודה בקצה השמאלי של הגרף הכתום היא נקודת ההתחלה של מורן (לפני השעה 8 וגם בכיוון הופכי לעמית). למשל:

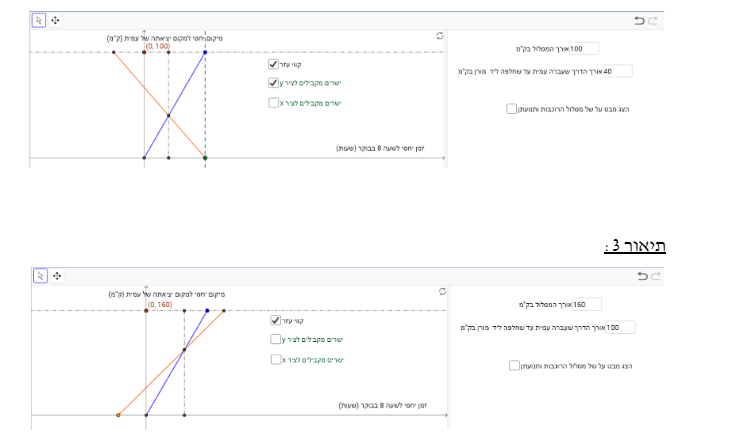
תיאור 3: 

מורן ועמית יצאו לרכיבה מאותו המקום במסלול שקבעו. עמית פגשה את מורן בשעה 11:00. מורן רכבה יותר מ- 3 שעות עד שחלפה ליד עמית.

כדי לקבל גרף מתאים לתיאור, קודם בוחרים אורך המסלול (למשל 160), מזיזים את הנקודה הכתומה לפני 0 (כי מורן יצאה לפני עמית), בוחרים אורך הדרך עד הפגישה (למשל 90)  כך שאם מחלקים את המספר ב 3 נקבל מספר בין 6-40  (כי נתון שהמהירות צריכה להיות בין 6 קמ"ש ל- 40 קמ"ש), ואז מתאימים את זמן הפגישה שיהיה בשעה 11 (לקבע את סליידר הזמן על 3 ואז להזיז את הנקודה הכחולה ימינה/שמאלה עד ששתי הנקודות האדומה והירוקה נפגשות בשעה 11)

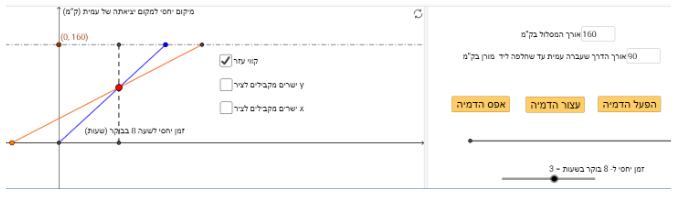
משימה 2

טענה 1 מתקיימת כאשר שתי הרוכבות יוצאות באותו כיוון (מאותה נקודת מוצא)

דוגמה שבה מורן יצאה לפני השעה 8 מאותו קצה:

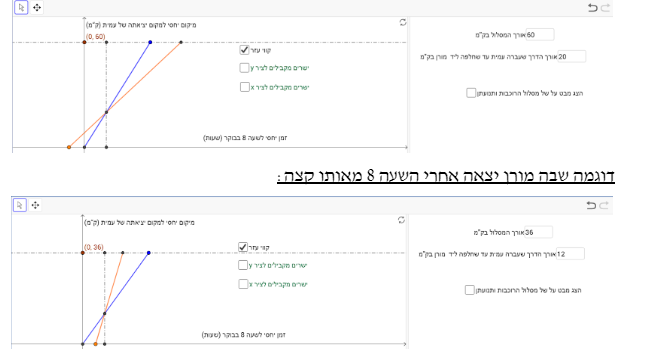
טענה 2 מתקיימת כאשר שתי הרוכבות יוצאות בכיוון הפוך – אחת לקראת השנייה.

דוגמה שבה מורן יצאה אחרי השעה 8 מהקצה השני: 

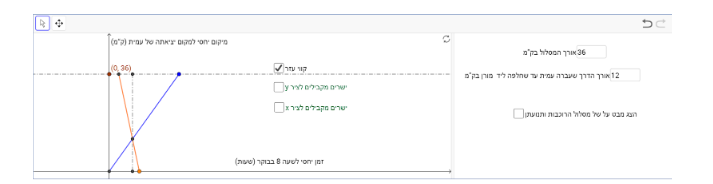
במקרה זה, רק תיאור 1 מתקיים. כלומר היחס בין הזמן שעמית רכבה ממקום יציאתה עד הפגישה לבין זמן הרכיבה שלה אחרי הפגישה עד שהגיע לסוף המסלול הוא 1:2, אך תיאור 2 לא מתקיים כי היחס בין הזמן שמורן רכבה ממקום יציאתה עד הפגישה לבין זמן הרכיבה שלה אחרי הפגישה עד שהגיע לסוף המסלול הוא 2:1 (ניתן להוכיח לפי משפט תאלס).

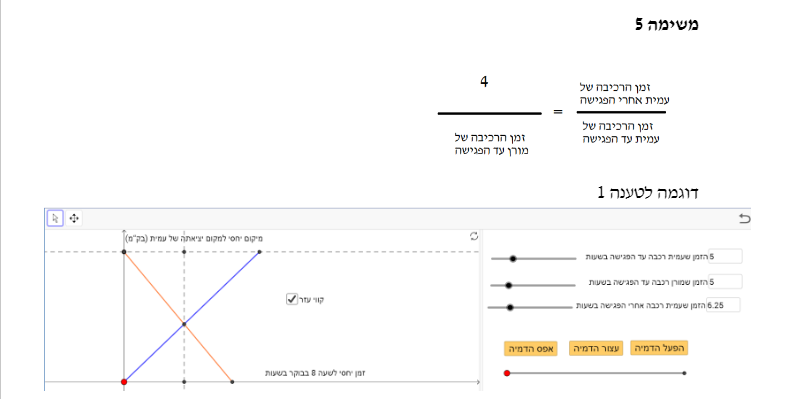
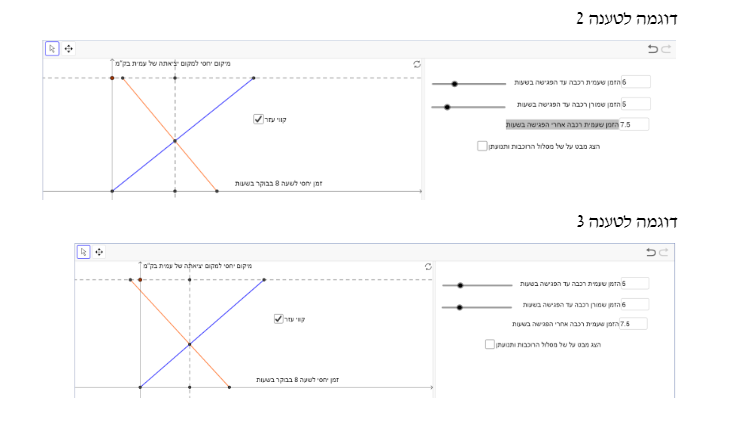
משימה 1:

תיאור 1: 

עמית עברה 30 ק"מ עד הפגישה

מורן יצאה מהקצה השני 

מורן יצאה לפני 8 

השתמשו בקווי עזר

תיאור 2:

מורן יצאה מהקצה השני 

מורן יצאה לפני 8 

השתמשו בקווי עזר

נכתב מספר קטן מ 50 ק"מ עד למפגש

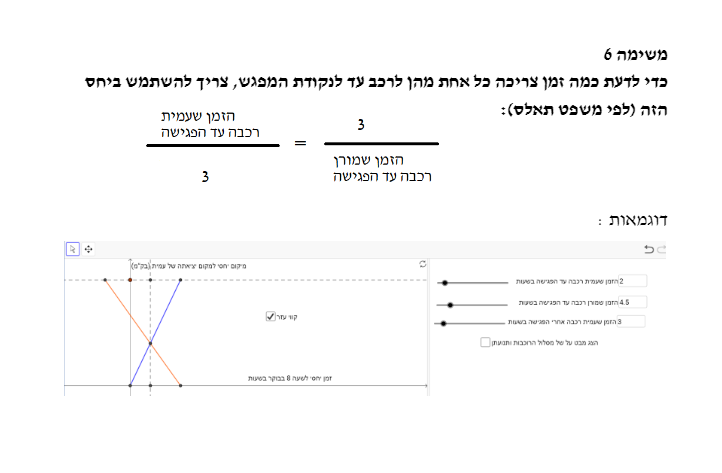
תיאור 3:

מורן יצאה מהקצה השני 

מורן יצאה לפני 8 

השתמשו בקווי עזר

המהירות של הרוכבות היא בין 6-40  קמ"ש

משימה 2 : 

הדוגמה מתאימה לנדרש

אורך המסלול מכפולות של 3

מורן יצאה בשעה 8

מורן יצאה לפני 8 

מורן יצאה מהקצה השני 

היחס הפוך (2:1)

השתמשו בקווי עזר

משימה 3: 

הדוגמה מתאימה לנדרש

מורן יצאה בשעה 8

מורן יצאה לפני 8 

מורן יצאה מהקצה השני 

היחס הפוך (2:1)

השתמשו בקווי עזר

משימה 4:

הדוגמה מתאימה לנדרש (היחס מתקיים)

מורן יצאה לפני עמית

מורן יצאה אחרי עמית

מורן יצאה מהקצה השני

השתמשו בקווי עזר

משימה 5:

הדוגמה מתאימה לנדרש (היחס מתקיים)

מורן יצאה אחרי עמית

מורן יצאה לפני עמית

השתמשו בקווי עזר

משימה 6:

הדוגמה מתאימה לנדרש

מורן יצאה אחרי עמית

מורן יצאה לפני עמית

השתמשו בקווי עזר

משימה 1:

• חשוב לוודא כי התלמידים מבינים איך הסימולציה עובדת ומה הקשר בין הערכים בחלון הימני לגרף בחלון השמאלי. 
• כדאי לדון עם התלמידים בדרכי הפתרון שלהם לתיאורים השונים. 

למשל, כדי לענות על תיאור 1 ישנן 2 דרכים לפתרון: 1) לפי חישוב חצי מרחק ( 60/2 = 30 )  או לפי חישוב מחצית הזמן ( ניתן להשתמש בסליידר הזמן). וכדי לענות על תיאור 3, צריך קודם לקבוע את אורך המסלול הכללי וגם את אורך הדרך שעברה עמית עד הפגישה (ראו פתרון בדוגמאות להגשה).

 משימה 2:

• מה הוא התנאי על נקודת המוצא של מורן כדי שכל אחת מהטענות תתקיים? 
• כדאי להוכיח למה היחס מתקיים ע"י דמיון משולשים ושימוש במשפט תאלס.

משימה 3 :

• כדאי לדון בדרכי הפתרון של התלמידים. במידה והם השתמשו בחישובים של מרחק/זמן/מהירות, אז כדאי להציע להם לפתור בעזרת היחס המתקבל מדמיון משולשים. 
• ישנה אפשרות לבדיקה עצמית באמצעות סליידר הזמן (היחס בין הזמנים שווה ליחס בין המרחקים).

משימה 4: 

חשוב לדון בתנאי שצריך להתקיים ומאיפה הוא נובע.

משימה 5:  

• חשוב לדון בתנאי שצריך להתקיים ומאיפה הוא נובע.

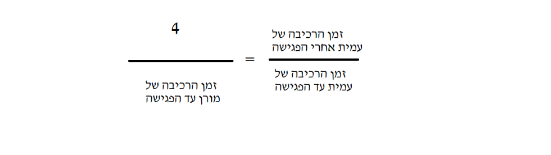
• האם שינוי אורך המסלול הכולל משנה את הפתרון?

משימה 6:

חשוב לדון בתנאי שצריך להתקיים ומאיפה הוא נובע.