המטרה של פעילות "שווה בשווה לגורמים של 30" היא לדון כיצד קובעים שמרובעים כלשהם (לאו דווקא מרובעים שדנים בהם בבית ספר) הם שווי שטח. בשונה מהפעילות המקדימה "שווה בשווה לגורמים של 8" אשר בה מפרקים מרובעים למשולשים, בפעילות זו תלמידים מפרקים מצולעים כלשהם למשולשים שווי שטח. 

גם פעילות זו עוסקת בזיהוי משולשים שווי שטח לפי צלע וגובה לצלע, ובחיבור שטחים (שטחי שני משולשים היוצרים שטח מרובע). כמו כן, ישנה התייחסות לחפיפות של מרובעים.

הקדמה למשימות:

קבוצת יזמים קנו מגרש ריבועי כך שמסביב למרכז המגרש יש אגם.

היזמים שוקלים  לחלק את המגרש לחלקות שוות שטח באמצעות קטעים היוצאים ממרכז השטח הריבוע אל צלעות השטח, כך שיתקבלו חלקות שוות שטח שכל אחת מהן כוללת חלק מהאגם.

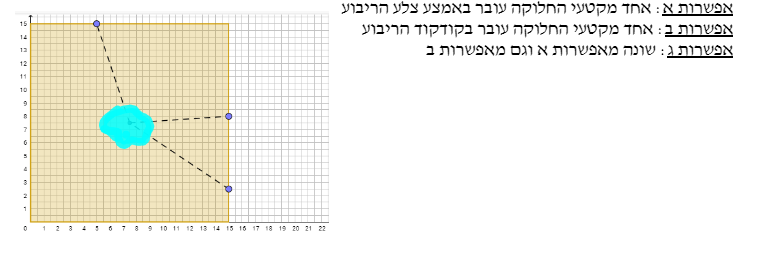
במשימה 1 נתון כי רון היזם  רצה לחלק את המגרש לשלוש חלקות שוות שטח באמצעות שלושה קטעים היוצאים ממרכז השטח הריבועי אל צלעות הריבוע (ראו ביישומון המצורף). רון התלבט בין שלוש  אפשרויות  לחלוקה כזו.

התלמיד מתבקש להזיז את הנקודות הכחולות ביישומון ולהגיש לכל אפשרות דוגמה תומכת.

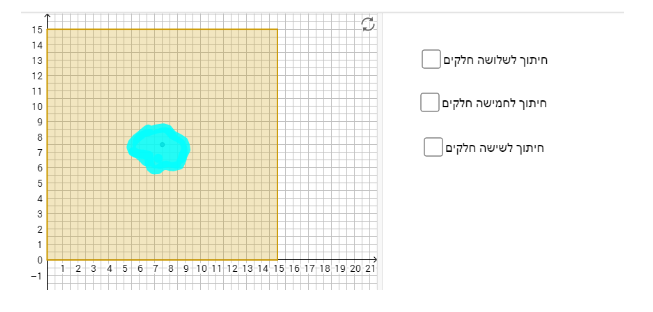
במשימה 2 נתון כי אפרת מקבוצת היזמים הציעה לחלק את המגרש לחמש חלקות שוות שטח באמצעות חמישה קטעים היוצאים ממרכז השטח הריבועי אל צלעות הריבוע (ראו ביישומון המצורף).

התלמיד מתבקש להזיז את הנקודות הכחולות בסרטוט ולהגיש שלוש תכניות שונות לחלוקת השטח לפי ההצעה של אפרת.

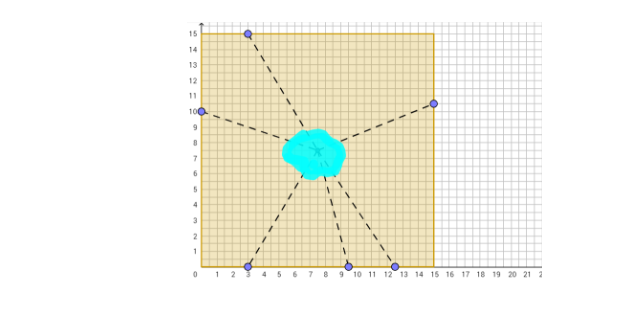
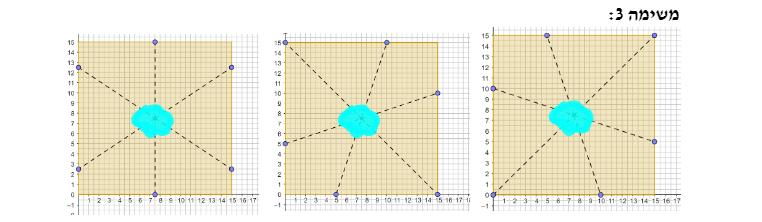
במשימה 3 נתון כי נורית מקבוצת היזמים  הציעה לחלק את המגרש לשש חלקות שוות שטח באמצעות שישה קטעים היוצאים ממרכז השטח הריבועי אל צלעות הריבוע (ראו ביישומון המצורף).

התלמיד מתבקש להזיז את הנקודות הכחולות בסרטוט ולהגיש שלוש תכניות שונות לחלוקת השטח לפי ההצעה של נורית.

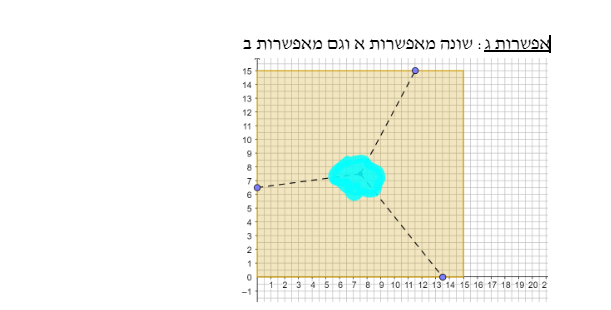
במשימה 4 נתון כי רני רצה לחלק את המגרש לחלקות שוות שטח באמצעות קטעים היוצאים ממרכז השטח הריבועי כך שיתקבלו זוגות של חלקות חופפות.

כמו כן, נתונות טענות. התלמיד מתבקש לסמן את הטענות הנכונות ולכל טענה נכונה להגיש דוגמה תומכת.

טענה 1: בחלוקת המגרש ל- 3 חלקות אפשר לקבל זוג של חלקות חופפות

טענה 2: בחלוקת המגרש ל- 5 חלקות אפשר לקבל בדיוק שני זוגות של חלקות חופפות

טענה 3: בחלוקת המגרש ל- 6 חלקות אפשר לקבל בדיוק שני זוגות של חלקות חופפות

הפעילות עוסקת בזיהוי משולשים שווי שטח לפי צלע וגובה לצלע, חיבור שטחים ושטחי מצולעים כלשהם. כמו כן, ישנה התייחסות לחפיפות של משולשים ומרובעים.

נושא שטח משולש נלמד בבית ספר יסודי ומתעמקים בו בכיתה ז' ביחד עם נושא שטחים של מצולעים כלשהם:

"המושג 'שטח' מוכר לתלמידים מבית הספר היסודי, אולם עקרונותיו עדיין אינם מובנים לרבים מהם."  (מתוך תוכנית הלימודים – עמ' 18)

"צורות חופפות שוות בשטחן, אבל צורות ששטחן שווה אינן בהכרח חופפות." (מתוך תוכנית הלימודים – עמ' 18)

"יש ללמוד לחשב את שטחו של מצולע על ידי חלוקתו למצולעים שאת שטחם אנחנו יודעים לחשב" (מתוך תוכנית הלימודים – עמ' 31)

 נושא חפיפת משולשים נלמד בכיתה ח', כך שלפי תוכנית הלימודים:

"יש ללמוד לזהות משולשים חופפים על פי שלושה נתונים מתאימים. " (מתוך תוכנית הלימודים – עמ' 65)

"יש לזהות בכלים קדם-דדוקטיביים משולשים החופפים זה לזה….. יש להבין כיצד לברר האם הנתונים לגבי משולשים אלה תואמים לאחד ממשפטי החפיפה" (מתוך תוכנית הלימודים – עמ' 116)

לכן פעילות זו מתאימה להעברה כפעילות תרגול בכיתה ח'-ט' עבור תלמידים אשר למדו את נושא חפיפת משולשים. 

שטח משולש

חיבור שטחים

חפיפת משולשים

משימה 1

אפשרות א: אחד מקטעי החלוקה עובר באמצע צלע הריבוע

אפשרות ב: אחד מקטעי החלוקה עובר בקודקוד הריבוע  

טענה 3: בחלוקת המגרש ל 6 חלקות אפשר לקבל בדיוק שני זוגות של חלקות חופפות.

לא נכון – תמיד מתקבלים 3 זוגות של חלקות חופפות.

משימה 1

דרישות המשימה: שלושת החלקות שוות שטח      

מאפייני עבודה: 

אחד מקטעי החלוקה עובר בקודקוד הריבוע 

אחד מקטעי החלוקה עובר באמצע צלע הריבוע

משימה 2

דרישות המשימה: חמשת החלקות שוות שטח      

מאפייני עבודה: 

אחד מקטעי החלוקה עובר בקודקוד הריבוע 

אחד מקטעי החלוקה עובר באמצע צלע הריבוע

משימה 3

דרישות המשימה: ששת החלקות שוות שטח      

מאפייני עבודה: 

שני קטעים מקטעי החלוקה יוצרים אלכסון בריבוע

שני קטעים מקטעי החלוקה עוברים באמצע צלעות נגדיות בריבוע 

משימה 4

טענה 1:

הוגשה דוגמה מתאימה לטענה

נבחרה טענה 1

המגרש חולק ל- 3 חלקות 

3 החלקות שוות שטח

קיים זוג של חלקות חופפות 

אחד מקטעי החיתוך חוצה אחת מצלעות הריבוע

אחד מקטעי החיתוך הוא חלק מאלכסון הריבוע

טענה 2:

הוגשה דוגמה מתאימה לטענה

נבחרה טענה 2 

המגרש חולק ל- 5 חלקות 

5 החלקות שוות שטח

קיימים בדיוק שני זוגות של חלקות חופפות 

אחד מקטעי החיתוך חוצה אחת מצלעות הריבוע

אחד מקטעי החיתוך הוא חלק מאלכסון הריבוע

טענה 3:

נבחרה טענה 3

המגרש חולק ל- 6 חלקות

6 החלקות שוות שטח

קיימים יותר משני זוגות של חלקות חופפות

שני קטעים מקטעי החלוקה יוצרים אלכסון בריבוע

שני קטעים מקטעי החלוקה עוברים באמצע צלעות נגדיות בריבוע

משימה 1

• • יש לדון באפשרויות השונות (אחד מקטעי החלוקה עובר באמצע צלע הריבוע, אחד מקטעי החלוקה עובר בקודקוד הריבוע)  ולנסות להגיע לכלל/לתנאי שצריך להתקיים על מנת לקבל חלקות עם שטחים שווים (הכלל: סכום הצלעות שעל היקף הריבוע צריך להיות שווה כלומר 60/3=20 ).
  • במקרה שאחד מקטעי החלוקה עובר באמצע צלע הריבוע – מה מאפיין שני הקטעים האחרים?  (צריכים להיות באותו מרחק – למה?)
  • איך ניתן להגיע לדוגמה תומכת באפשרות ג ? כלומר שקטעי החלוקה לא עוברים באמצע צלע הריבוע ולא בקודקוד הריבוע וגם שלושת החלקות שוות שטח? (תשובה: אחרי שמוצאים תשובה תומכת באחת האפשרויות א או ב, מזיזים כל קטעי החיתוך באותה מידה לאותו כיוון)

• יש לעורר דיון לגבי אופן הוכחת שוויון השטחים:

(א) ניתן להוכיח מקרה א באמצעות חישובי שטחים של המשולשים והמלבנים המתקבלים מפירוק המצולעים. 

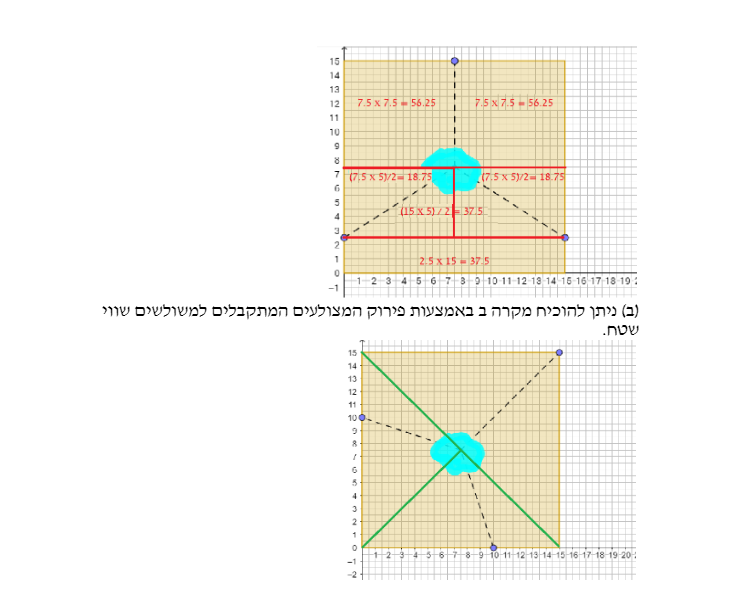
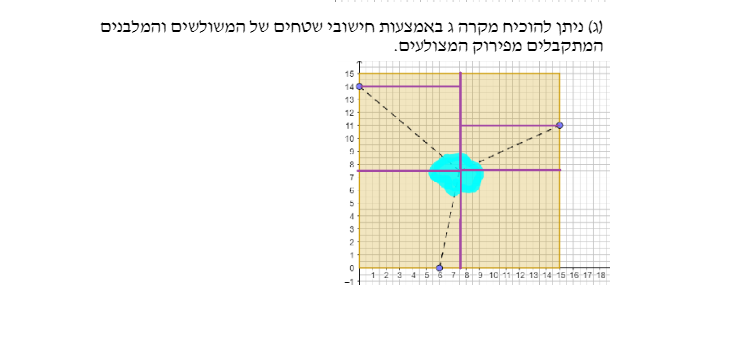
משימה 2 

• • יש לדון באפשרויות השונות (אחד מקטעי החלוקה עובר באמצע צלע הריבוע, אחד מקטעי החלוקה עובר בקודקוד הריבוע)  ולנסות להגיע לכלל/לתנאי שצריך להתקיים על מנת לקבל חלקות עם שטחים שווים (הכלל: סכום שתי הצלעות שעל היקף הריבוע צריך להיות שווה כלומר 60/5=12 ).

• יש לעורר דיון לגבי אופן הוכחת שוויון השטחים – באמצעות פירוק המצולעים המתקבלים למשולשים שווי שטח.

• ניתן להשתמש בחפיפת משולשים כדי להוכיח את שוויון שטחיהם.
• במקרה ומתקבלים מצולעים חופפים וגם שווי שטח, האם הזזת כל קטעי החיתוך באותה מידה לאותו כיוון ששומרת על "שוויון בשטחים" מאפשרת גם שמירה על "חפיפות המצולעים" ? 

משימה 3 

• • יש לדון באפשרויות השונות (שניים מקטעי החלוקה יוצרים אלכסון בריבוע, שניים מקטעי החלוקה חוצים צלעות נגדיות בריבוע)  ולנסות להגיע לכלל/לתנאי שצריך להתקיים על מנת לקבל חלקות עם שטחים שווים (הכלל: סכום שתי הצלעות שעל היקף הריבוע צריך להיות שווה כלומר 60/6=10 ).

• יש לעורר דיון לגבי אופן הוכחת שוויון השטחים – באמצעות פירוק המצולעים המתקבלים למשולשים שווי שטח.

• כמה זוגות של חלקות חופפות מתקבלים במקרה והמגרש חולק לחלקות שוות שטח? האם ניתן לחלק בצורה שונה ולשמור על שוויון השטחים אך יתקבל רק זוג אחד של חלקות חופפות? 

משימה 4

• מתי מקבלים זוג של חלקות חופפות כאשר מחלקים את המגרש ל 3 חלקות שוות שטח? 
• מתי מקבלים בדיוק 2 זוגות של חלקות חופפות כאשר מחלקים את המגרש ל 5 חלקות שוות שטח? 
• כמה זוגות של חלקות חופפות מתקבלים כאשר מחלקים את המגרש ל 6 חלקות שוות שטח? האם אפשר לקבל פחות מ- 3 זוגות חופפות? 
• אפשר לדון בהוכחת החפיפה של החלקות.